سپیس ٹائیم

اک مختصر حصہ سارانش لئی اتھے کلکّ کرو
نوٹ: اندرونی وکیپیڈیا-سمپرکاں والے نیویگیشن مثلیاں توں بچن لئی، موبائیل فون ورتونکاراں نوں چاہیدا اے کہ حصہ شارانشاں توں سارے حصیاں نوں جان-پچھان تک واپس پہلاں توں ہی پھیلا لین ۔

چتر 1-2. مائکلسن اتے مورلے نوں امید سی کہ ایئتھر راہیں رفتار، اپنے ینتراں دیاں دوویں باہاں نوں پار کرن والے پرکاش درمیان اک ڈپھرینشیئل فیز شفٹ پیدا کردی اے، جسدے نیگٹو نتیجے دی سبھ توں زیادہ لوجیکل وضاحت، ایئتھر ڈریگنگ، تاریاں دے رستے توں ہٹن دے معائنہ دے مطابق نہیں اے۔

مدھ-1800ویں دہاکے توں، آراگو سپوٹ اتے ہوا بنام پانی وچ پرکاش دی سپیڈ دے ڈپھرینشیئل ناپاں دے معائنہ دے روپ وچ کیتے گئے کئی پریوگاں ولوں کورپیوسکیولر تھیوری توں الٹ پرکاش دی ترنگ پھترت سدھ کیتی گئی منی جاندی رہی سی۔^[۹] ترنگاں توں مطلب سی کسے زریعہ دی ہوند جو ترنگاں بناؤندا سی، پر ایہناں پریوگاں دے نتیجیاں وجوں نظریاتی چمکدار ایئتھر دیاں خاصیتاں نوں ناپن دے یتناں نے ورودھابھاس والے نتیجے مہیا کروائے۔ اداہرن دے طور تے، 1851 دے پھزیاؤ استعمال نے ثابت کیتا کہ وہِ راے پانی اندر پرکاش دی سپیڈ ہوا وچ پرکاش دی سپیڈ اتے پانی دی سپیڈ دے جوڑ نالوں پانی دے رپھریکشن انڈیکس اتے مشتمل مقدار جنی گھٹ سی۔

ہور مثلیاں وچکار، ریپھریکشن (جو ویولینتھ اتے انحصار اے) دے انڈیکس اتے اس استعمال دے نتیجیاں وجوں ملی انشک ایئتھر-ڈریگنگ دی نربھرتا نے سخت نتیجے ول لجاندا کہ ایئتھر تتدور طور تے پرکاش دے وکھرے رنگاں واسطے وکھریاں سپیڈاں نال وہندا اے۔ ^[۱۰]

1887 دے مشہور مائیکلسن-مورلیسن استعمال (Fig. 1‑2) نے دھرتی دیاں گتیاں دے اتے کوئی ڈپھرینشیئل اثر نہیں دکھایا، بھاویں پرکاش دی سپیڈ اتے نظریاتی ایئتھر، اتے سبھ توں زیادہ ممکن وضاحت، مکمل ایئتھر ڈریگنگ، ستھیلر ابیریشن دے معائنہ نال میل نہیں کھاندی سی۔ (Fig. 1‑3)۔^[۱۱]

چتر 1-3. (top) سٹیلر ابیریشن دی سمت سال دے وکھرے سمیاں اتے وکھری ہندی اے۔ (bottom) ایئتھر ڈریگنگ—تھیوری جو اک وار پرکاش دی سپیڈ اتے ایئتھر دے پرجذبات نوں پچھانن پرتِ ااہلیت نوں سمجھاؤن واسطے ترقی یافتہ کیتی گئی سی- سٹیلر ابیریشن نال میل نہیں کھاندی اے۔^{[وادھو ویرویاں واسطے اتھے کلکّ کرو ۱]}

1889 وچ جورج پھرانسس پھٹزگرالڈ اتے 1892 وچ ہینڈرک لورنٹز نے آزاد طور تے تجویز رکھیا کہ ستھر کیتے ہوئے ایئتھر راہیں سفر کردیاں پدارتھک وستواں بھوتکی طور تے اپنے لانگھے ولوں متاثر ہندیاں ہن، انی کو مقدار جنا رفتار دی سمت دا خلاف کردا اے، جو مائیکلسن-مورلیسن استعمال دے نیگٹو نتیجیاں نوں سمجھاؤن لئی لازمی سی۔ (رفتار دی سمت دے سمکون والیاں سمتاں وچ کوئی لمبائی تبدیلی نہیں واپردی۔) 1904 توں، لورنٹز نے اپنی تھیوری وچ اسطراں پھلار کیتا کہ اسنے اوہناں اکئیشناں نال رسمی طور تے ملدیا جلدیاں اکئیشناں دی حصول کیتی جہناں نوں بعد وچ آئینسٹائین نے ویونتبند کیتا (یانِ کہ، لورنٹز ٹرانسپھورم)، پر بنیادی طور تے ذرا وکھری وضاحت نال ویونتبند کیتا۔

ڈائنامکس (پھورساں اتے ٹورکاں ایے رفتار اتے ایہناں دے پرجذبات دے مطالعہ) دی اک تھیوری دے طور تے، اسدی تھیوری نے مادہ دے بھوتکی رچنہاریاں دے اصلی بھوتکی تروڑ-مروڑ نوں منیا، اتے اسنے معائنہ کیتے جا سکن یوگ وکھ وکھ بھوتکی پرجذبات دا اندازا لگایا۔^[۱۲]^:163–174 اداہرن دے طور تے، زیادہتر بھوتک سائنسداناں دا مننا سی کہ لورنٹز کنٹریکشن ٹرؤٹن-نوبلن ایکسپیریمینٹ جاں ریلیگھ اتے بریس دے استعمالاں ورگے اجیاے پریوگاں ولوں پچھانمیوگ ہو سکدا ہونا چاہیدا اے۔^[۱۳]^:64 پھیر وی، اسدے نیگٹو نتیجے ملے، اتے الیکٹرون دی اسدی 1904 دی تھیوری اندر، لورنٹز نے ایہناں نیگٹو نتیجیاں بارے سمجھایا کہ ایہہ اسدیاں ٹرانسپھورماں دے اک لازمی نتیجے وجوں سن۔ پوآئنکیئر نے، لورنٹز تجزیہ وچ کجھ غلطیاں سدھاردیاں ثابت کیتا کہ ایئتھر پچھانیا نہیں جا سکدا، پر اسنے اپنی زندگی دے رہندے وقت دوران لورنٹز ٹرانسپھورم دی ڈائنیمیکل وضاحت وچ یعقین کرنا جاری رکھیا۔^[۱۲]^:163–174

فزکس وچ حال ترقی یافتہ سمجھ، 20ویں-صدی دے مکن دی لمبے ویلے توں حاصل کیتی جا رہی تھاں ول جھکاؤ رکھدی جاندی اے جو مائیکلسن اتے مورلے استعمال اتے اے۔ پر آئینسٹائین لئی، اسدی آخری پریرنا اوہ بیمیلتاواں رہیاں ہن جو اسنے اوس انداز وچ سمجھیاں سن جس وچ الیکٹرومیگنٹزم دی میکسویلّ دی تھیوری ویاکھئت کیتی گئی سی۔ بھاویں 1905 وچ، آئینسٹائین نے رفتار شیل چمبک اتے کنڈکٹر مسئلہ بارے لکھیا جسنوں عامطور تے اسمروپتاواں وال لجاندا سمجھیا گیا سی، پھیر وی ایہہ اسمروپتاواں ہرٹز، لورنٹز، اتے خود میکسویلّ سمیت، میکسویلّ دی تھیوری دے پرمکھ سپوٹراں وچوں کسے ولوں منگی جاندی وضاحت منگدے اک اہم مصلے دے طور تے نوٹ کیتیاں جاندیاں نہیں لگدیاں۔^[۱۳]^:135–142

آئینسٹائین دی سپیشل رلیٹیوٹی دی تھیوری، جو 1905 وچ پیش کیتی گئی سی، نے ایہناں اتے ہور وڈے فزکس رازاں دا اک مکمل حل مہیا کروایا، اتے اسنے اجہیاں بھوکھبانیاں شروع کیتیاں جو وار وار ثابت ہندیاں رہیاں ہن۔ آئینسٹائین نے اپنا تجزیہ کائنامیٹکس (پھورساں دی ریپھرینس توں بغیر رفتار شیل چیزاں دے مطالعہ) دی بولی وچ کیتا نہ کہ ڈائنامکس دی بولی وچ۔ ایہہ لگدا ہو سکیگا کہ اسنے سپیسٹائیم بارے پہلاں جیؤمیٹریکل طور تے نہیں سوچیا سی۔ ایہہ آئینسٹائین دا پہلا گنت پروپھیسر حرمن منکووسکی سی، جسنے سپیشل رلیٹیوٹی دی اک جیؤمیٹریکل وضاحت مہیا کرواؤنی سی۔^[۱۴]^:219

آئینسٹائین شروع وچ سپیشل رلیٹیوٹی دی جیؤمیٹریکل وضاحت نوں خارج کردا رہا سی تے اسنوں überflüssige Gelehrsamkeit (ضرورت توں زیادہ علم) پکاردا رہا سی۔ پھیر وی، سپیشل رلیٹیوٹی دی جیؤمیٹریکل وضاحت نے جنرل رلیٹیوٹی دے آئینسٹائین دے بعد دے ترقی پرتِ اہم رول نوں ثابت کرنا سی، اتے 1916 وچ، آئینسٹائین نے پوری طرحاں منکووسکی پرتِ اپنی اہسانمندی قبول کیتی، جسدی وضاحت نے جنرل رلیٹیوٹی پرتِ پرورتن نوں وڈے پدھر تے مدد کیتی۔^[۱۲]^:151–152 سپیشل رلیٹیوٹی دا سپیسٹائیم ادوں توں منکووسکی سپیسٹائیم دے طور تے جانیا جاندا رہا اے۔

ہینڈرک لورنٹز

ہینری پوآئنکیئر

البرٹ آئینسٹائین

حرمن منکووسکی

Figure 1-3.

اک اہم اداہرن ہینری پوآئنکیئر اے،^[۱۵]^[۱۳]^{:73–80,93–95} جسنے 1898 وچ ترک دتا کہ دو واقعے دی تتکالینتا اک پرمپرا دا مصلیٰ اے۔^[۱۶]^{[note ۲]} 1900 وچ، اسنے پچھانیا کہ لورنٹز دا لوکل ٹائم دراصل اوہ سماں ہندا اے جو پرکاش دی سپیڈ نوں ستھر مندے ہوئے کلوک سنکرونائزیشن دی اک واضع عملی تشریح لاگوُ کردے ہوئے رفتار شیل کلوک دندے ہن۔^{[note ۳]} 1900 اتے 1904 وچ، اسنے اوس چیز دی پرمانکتا تے زور دندے ہوئے ایئتھر دی جنمجات پچھان-ااہلیت سجھائی، جس نوں اسنے رلیٹیوٹی دا اصول کیہا، اتے 1905/1906 وچ^[۱۷] اسنے گنتک طور تے رلیٹیوٹی دے سوے-سدھ اصول مطابق کرن واسطے الیکٹروناں دی لورنٹز تھیوری نوں مکمل بنایا۔ لورنٹز انویریئنٹ گریویٹیشن اتے وکھ وکھ پرکلپناواں دی چرچہ کردے وقت، اسنے پھور-پجیسن، پھور-ولوسٹی، اتے پھور-فورس نامک وکھ وکھ فور-ویکٹراں نوں متاثر کردے ہوئے اک 4-ایامی سپیسٹائیم دا نوین تجزیہ پیش کیتا۔^[۱۸]^[۱۹] اسنے، پھیر وی، اگلے پیپراں وچ 4-ایامی فارمولا ویونتبندی دا پچھا نہیں کیتا، تے کیہا کہ ریسرچ دی ایہہ لائن “محدود لابھ واسطے وڈی تکلیف ضروری” کردی لگدی اے، تے انت نوں ایہہ نتیجہ کڈھیا کہ تنّ-ایامی بولی ساڈے دنیا دے ویروے پرتِ سبھ توں زیادہ ڈھکویں لگدی اے۔^[۱۹] ہور اگے، 1909 جنی دیر بعد، پوآئنکیئر نے لورنٹز ٹرانسپھورم دی گتیشیلاتمک وضاحت وچ وسواس رکھنا جاری رکھیا۔^[۱۲]^:163–174 ایہناں اتے ہور کارناں کرکے، سائنس دے زیادہتر اتہاسکار ترک کردے راے ہن کہ پوآئنکیئر نے اوہ نہیں کھوجیا جس نوں ہن سپیشل رلیٹیوٹی کیہا جاندا اے۔^[۱۳]^[۱۲]

1905 وچ، آئینسٹائین نے سپیس اتے ٹائم دی اک تھیوری دے طور تے اسدی اجوکی سمجھ مطابق سپیشل رلیٹیوٹی پیش کیتی (بھاویں سپیسٹائیم فارمولا ویونتبندی دیاں تکنیکاں ورتیں بغیر)۔^[۱۳]^[۱۲] جدونکھ اسدے نتیجے گنتک طور تے لورنٹز اتے پوآئنکیئر دے نتیجیاں نال ملدے ہن، پھیر وی ایہہ آئینسٹائین ہی سی۔ جسنے ثابت کیتا کہ لورنٹز ٹرانسپھورمیشناں مادہ اتے ایئتھر درمیان پرسپر کریاواں دا نتیجہ نہیں ہن، سگوں خود سپیس اتے ٹائم دی قدرت نال متعلق ہن۔ آئینسٹائین نے اپنا وسلیشن ڈائنامکس نالوں کائنامیٹکس دی بولی وچ کیتا۔ اسنے اپنے سارے نتیجے ایہہ پچھاندے ہوئے حاصل کیتے کہ ساری دی ساری تھیوری دو سوے-سدھ نظریات اتے بنائی جا سکدی اے: رلیٹیوٹی دا اصول اتے پرکاش دی سپیڈ دی استحکام دا اصول۔ اسدے نال نال، آئینسٹائین نے 1905 وچ سرو عام پنج اتے توانائی برابری پیش کردے ہوئے اک الیکٹرومیگنیٹک پنج-توانائی تعلق دے پچھلے یتناں نوں دبا دتا، جو 1907 وچ برابری اصول دی اسدی اگلی فارمولا ویونتبندی واسطے معاون رہا سی۔، جسنے انرسیئل اتے گریویٹیشنل پنج اعلان کیتا۔ پنج-توانائی برابری ورتدے ہوئے، اسدے نال نال، آئینسٹائین نے دکھایا، کہ کسے وستو دا گریویٹیشنل پنج اسدی توانائی سامان دے انوپات وچ ہندا اے، جو جنرل رلیٹیوٹی ترقی یافتہ کرن وچ شروعاتی نتیجیاں وچوں اک نتیجہ سی۔ جدونکھ ایہہ دسدا ہو سکدا اے کہ اسنے سبھ توں پہلاں جیؤمیٹریکل طور تے سپیسٹائیم بابت نہیں سوچیا سی،^[۱۴]^:219 پھیر وی جنرل رلیٹیوٹی دے ہور اگے ترقی وچ آئینسٹائین نے سپیسٹائیم فارمولا ویونتبندی نوں پوری طرحاں سامل کر لیا سی۔

جدوں آئینسٹائین نے 1905 وچ چھاپیا، تاں اکہور پرتییوگی، اسدا پہلا گنت پروپھیسر حرمن منکووسکی، وی سپیشل رلیٹیوٹی دے زیادہتر بنیادی تتاں اتے اپڑیا سی۔ میکس بورن نے منکووسکی دا ودیارتھ-سہویوگک ہون واسطے منکووسکی نال اک میٹنگ دا پنر-پربندھ کیتا:^[۲۰]

“

I کولوگنِ گیا، منکووسکی نوں ملیا اتے 2 ستمبر 1908 نوں اسدا دتا جا رہا لکچر “سپیس اتے ٹائم” سنیا۔ […] اسنے مینوں بعد وچ دسیا کہ اسنوں اودوں وڈا جھٹکا لگا جدوں آئینسٹائین نے اپنا اوہ پیپر چھاپیا جس وچ اک دوجے پرتِ ساپیکھک رفتار شیل اؤبزروراں دے وکھرے لوکل وقتاں دی برابری اچاری گئی سی؛ جس واسطے اس ایہی نتیجیاں اتے آزاد طور تے پہنچیا سی۔ پر اسنے چھپوایا نہیں کیونکہ اوہ پہلاں اسنوں ہریک طریقے نال شاندار طور تے گنتک بنتر کڈھکے پیش کرنا پسند کردا سی۔ اسنے کدے وی پہل دا دعوہ نہیں کیتا اتے ہمیشاں ہی مہان کھوج وچ اسدی پوری سانجھ آئینسٹائین نوں دندا رہا۔

”

منکووسکی 1905 دیاں گرمیاں توں مائیکلسن دے ہانیکار پریوگاں توں بعد الیکٹروڈائنامکس دی حالت نال متعلق رہا سی، جدوں منکووسکی اتے ڈیوڈ ہلبرٹ نے لورنٹز، پوآئنکیئر اتے ہوراں دے پیپراں دا مطالعہ کرن واسطے سمکالین مشہور بھوتک سائنسداناں ولوں اک اڈوانسڈ سیمینار دی حاضری بھرن دی اگوائی کیتی سی۔ پھیر وی، ایہہ پوری طرحاں واضع نہیں اے کہ کدوں منکووسکی نے سپیشل رلیٹیوٹی دی جیؤمیٹریکل فارمولا ویونتبندی نوں ویونتبند کرنا سرو کیتا سی جسنے اسدا نام پیدا کرنا سی، جاں اوہ لورنٹز ٹرانسپھورمیشناں دی پوآئنکیئر دی چار-ایامی وضاحت توں کنا کو متاثر ہویا سی۔ ناں ہی ایہہ ہی واضع ہویا اے کہ جیکر اسنے کدے لورنٹز ٹرانسپھورمیشناں پرتِ سمجھ پرتِ آئینسٹائین دے تنقیدی یوگدان دی ایہہ سوچدے ہوئے پوری طرحاں تعریف وی کیتی ہووے، کہ آئینسٹائین دا کم لورنٹز دے کم دی اک شاخاں ہووے۔^[۲۱]

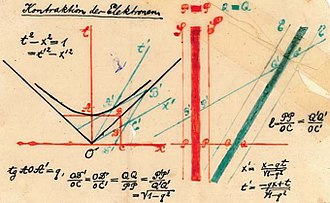
اپنی موت توں سال کو توں تھوڑا چر پہلاں، منکووسکی نے نومبر 5, 1907 نوں “دی رلیٹیوٹی پرنسپل” (Das Relativitätsprinzip) سرلیکھ ماتحت گوٹنگٹن میتھیمیٹیکل سوسائٹی نوں دتے اک لیچکر وچ سپیسٹائیم دی اپنی جیؤمیٹریکل وضاحت جنتا اگے پرسعنصر کیتی۔ اس لکچر دے مول ورژن وچ، منکووسکی نے ایئتھر ورگے پرانے شبداں دی ورتوں جاری رکھی، پر “انالز آف پھزکس” (Annalen der Physik) وچ اس لکچر دے 1915 والے اسدے مرنوصوبہ پرکاشن نوں اس شبد نوں ہٹاؤن لئی سومرفیلڈ نے ایڈٹ کیتا سی۔ سومرفیلڈ نے اس لکچر دے شائع روپ نوں وی ایڈٹ کیتا، تاں جو منکووسکی دی آئینسٹائین والی ججمینٹ دوہرائی جا سکے جس وچ رلیٹیوٹی دے اصول دا آئینسٹائین نوں صرف سپشٹکرتا ہی کیہا گیا سی، جو اسدا مکھ ویاکھیاکار سی۔^[۲۰]

دسمبر 21, 1907 نوں، منکووسکی نے پھیر توں گوٹنگٹن سینٹیپھک سوسائٹی موہرے بولیا، اتے ستمبر 21, 1908 نوں، منکووسکی نے اپنی مشہور گل بات، سپیس اینڈ ٹائم (Raum und Zeit)،^[۲۲] جرمن سوسائٹی آف سائنٹسٹس اینڈ پھزیشیئنز اگے پیش کیتی۔^{[note ۴]}

“سپیس اتے ٹائم” دے شروعاتی سبد منکووسکی دی مشہور بیانبازی سامل کردا اے کہ “اسلئی، سپیس اپنے آپ وچ، اتے ٹائم اپنے آپ وچ صرف کسے پرچھاویں تک پوری طرحاں گھٹ کے محدود ہو جانگے، اتے دوواں دی یونین دی کوئی قسم آزادی سرکھات رکھیگی۔”

سپیس اتے ٹائم نے سپیسٹائیم چتراں (Fig. 1‑4) دی پہلی عوامی پیش کش شامل کیتی سی، اتے اک اہم مظاہرہ شامل کیتا سی۔ کہ “ستھر انترال” دی دھارنا، اس انوبھوَ-سدھو معائنہ نال کہ پرکاش دی سپیڈ محدود ہندی اے، سپیشل رلیٹیوٹی دی سمپورنتا دی ویونتبندی دی آگیا دندی اے۔^{[note ۵]}

آئینسٹائین، اپنے ولوں، سپیشل رلیٹیوٹی دی منکووسکی دی جیؤمیٹریکل وضاحت نوں پہلاں خارج کردا سی۔، تے اسنوں überflüssige Gelehrsamkeit (ضرورت توں زیادہ علم) کہندا سی۔ پھیر وی، 1907 وچ سرو کیتی جان والی جنرل رلیٹیوٹی واسطے اسدی ریسرچ نوں پوری کرن دے چکر وچ، رلیٹیوٹی دی جیؤمیٹریکل وضاحت اہم ہونی ثابت ہو گئی، اتے 1916 وچ، آئینسٹائین نے منکووسکی پرتِ اپنی شنکا پوری طرحاں قبول کر لئی، جسدی وضاحت نے جنرل رلیٹیوٹی پرتِ تبدیلی نوں بہت سودھا حاصل کیتی۔ ^[۱۲]^:151–152 کیونکہ سپیسٹائیم دیاں ہور قسماں وی ہندیاں ہن، جویں جنرل رلیٹیوٹی دا وکرت سپیسٹائیم، اسلئی سپیشل رلیٹیوٹی دا سپیسٹائیم اجکل “منکووسکی سپیسٹائیم” دے نامک نال جانیا جاندا اے۔ جان-پچھان ول پرتو

سپیشل رلیٹیوٹی وچ سپیسٹائیم

سپیسٹائیم عرصے

تنّ-ایاماں اندر، دو نقطےآں درمیان دوری نوں پائیتھاگوریئن تھیورم ورتدے ہوئے متاثر کیتا جا سکدا اے:

{\left(\Delta {d}\right)}^{2}={\left(\Delta {x}\right)}^{2}+{\left(\Delta {y}\right)}^{2}+{\left(\Delta {z}\right)}^{2}

بھاویں دو درشک، وکھرے “کو-آرڈینیٹ سسٹم” ورتدے ہوئے دو نقطےآں دی x,y, اتے z پوزیشن نوں ناپ سکدے ہن، پھیر وی نقطےآں درمیان دوری دوواں ناظرین واسطے اکو جہی رہیگی (ایہہ مندے ہوئے کہ اوہ اکو جہیاں یونٹاں ورت کے ناپ راے ہن)۔ دوری "انویریئنٹ (ستھر) رہندی اے۔

سپیشل رلیٹیوٹی اندر، پھیر وی، دو نقطےآں درمیان دوری، لورنٹز کنٹریکسن صدقہ اکو جہی نہیں رہندی جیکر دو ناظرین ولوں، ادوں ناپی جاوے جدوں اک درشک رفتار کر رہا ہووے۔ پرحالت ہور وی زیادہ گنجھل دار بن جاندی اے جیکر دوویں نقطہ وقت دے نال نال سپیس وچ وی وکھرے وکھرے ہون۔ اداہرن دے طور تے، جیکر اک درشک کسے ستھان اتے واپر رہیاں دو واقعے نوں اکو ستھان تے دیکھدا اے، پر وکھرے وکھرے وقت تے دیکھدا اے، تاں پہلے درشک دے حوالہ وچ رفتار شیل کوئی دوجا انسان دوویں واقعے نوں وکھرے ستھاناں تے واپردا دیکھیگا، کیونکہ (اوہناں دے نظرئیے توں) اوہ سٹیشنری ہندے ہن، اتے گھٹنا دی پجیسن نیڑے آ رہی جاں دور جا رہی ہندی اے۔ اسطراں، دو واقعے درمیان پربھاوی دوری نوں ناپن واسطے اک وکھرا ناپ ورتیا جانا ضروری ہو جاندا اے۔

چار-ایامی سپیسٹائیم اندر، دوری دا تلّ عرصہ ہندا اے۔ بھاویں ٹائم اک چوتھے ایام دے روپ وچ آؤندا اے، پھیر وی اسنوں مقامی ایاماں توں وکھرے طریقے نال ورتیا جاندا اے۔ منکووسکی سپیس اسے کارن چار-ایامی یکلڈن سپیس توں اہم پہلوآں وچ وکھری ہندی اے۔ سپیس اتے ویلے نوں سپیسٹائیم وچ جڑ دین دا بنیادی کارن ایہہ اے کہ سپیس اتے ٹائم وکھرے طور تے انویریئنٹ نہیں ہندے، دوجے شبداں وچ، ڈھشاعراں حالتاں وچ، وکھرے درشک دو واقعے درمیان وقت دی لمبائی اتے (ٹائم ڈلیشن کارن) جاں دوویں واقعے درمیان دوری اتے (لینتھ کنٹریکسن کارن) اسہمت رہنگے۔ پر سپیشل رلیٹیوٹی سپیسٹائیم عرصہ نامک اک نواں انویریئنٹ مہئیا کرواؤندی اے، جو سپیس وچ اتے ٹائم وچ دوریاں نوں ملاؤندا اے۔ ساودھانی نال وقت اتے دوری ناپن والے سارے درشک کسے وی دو واقعے درمیان اکو جیہا سپیسٹائیم عرصہ کھوجنگے۔

منّ لؤ اک اؤبزرور اجہیاں دو واقعے ناپدا اے جو وقت وچ $\Delta t$ اتے اک مقامی دوری $\Delta x$ راہیں وکھریاں ہندیاں ہن۔ پھیر دوویں واقعے درمیان سپیسٹائیم عرصہ ${\left(\Delta {s}\right)}^{2}$ سپیس وچ اک دوری $\Delta {x}$ اتے وقت وچ اک عرصہ $\Delta {t}$ راہیں وکھریاں واپردیاں ہن:

(\Delta s)^{2}=(\Delta ct)^{2}-(\Delta x)^{2}

(جاں تن سپیس ڈائمینشناں واسطے،

(\Delta s)^{2}=(\Delta ct)^{2}-(\Delta x)^{2}-(\Delta y)^{2}-(\Delta z)^{2}

)

ستھرانک ${\textrm {c}}$ ، پرکاش دی سپیڈ، دوری ناپن واسطے ورتیاں جاندیاں یونٹاں (میٹراں) نوں، وقت نوں ناپن واسطے ورتیاں جاندیاں یونٹاں (سکنٹاں) وچ تبدیل کردا اے۔

بھاویں سنکھیپیؤ لئی، عرصہ سمیکرناں نوں ڈیلٹیاں توں بغیر ہی دیکھیا جاندا اے، جو اگے دی جئداتر چرچہ وچ وی سامل اے، پھیر وی سرو عام طور تے ایہہ سمجھ لینا بندا اے کہ، $x$ دا مطلب اے $\Delta {x}$ ، وغیرہ۔ ساڈا واسطہ ہمیشاں ہی دو واقعے نال متعلق امستقل نردیشانک ملاں جاں ستھاناں دے انتراں نال پیندا اے، اتے کیونکہ کوئی وی ترجیح والا مول نقطہ (ارجن) نہیں ہندا، اسلئی اکلوتا نردیشانک ملّ کوئی لازمی مطلب نہیں رکھدا۔

اپر درسائی اکئیشن پائیتھاگوریئن تھیورم نال ملدی جلدی اے، صرف $({\textrm {c}}\,t)^{2}$ اتے $x^{2}$ رقماں درمیان اک مائینس دے چنہ دا ہی فرق اے۔ ایہہ وی نوٹ کرو کہ سپیسٹائیم عرصہ مقدار $s^{2}$ ہندی اے، نہ کہ خود $s$ । کارن ایہہ اے کہ یکلڈن جیؤمیٹری وچ دوریاں توں الٹ، منکووسکی سپیسٹائیم اندر عرصے نیگٹو وی ہو سکدے ہن۔ نیگٹو سنکھیاواں دے ورگمولاں نال ورتن دی جگہ، بھوتک سائنسدان رسمی طور تے $s^{2}$ نوں کسے چیز دے طبقہ ہون نالوں، اپنے آپ وچ اک نرالا چنہ مندے ہن۔^[۱۴]^:217

مائینس چنہ دے کارن، دو وکھریاں واقعے درمیان سپیسٹائیم عرصہ زیرو ہو سکدا اے۔ جیکر $s^{2}$ پوزٹو ہووے، تاں سپیسٹائیم عرصہ ٹائیملائیک کہاؤندا اے، جسدا مطلب اے کہ دو واقعے سپیس نالوں ٹائم راہیں زیادہ وکھریاں ہن۔ جیکر $s^{2}$ نیگٹو ہووے، تاں سپیسٹائیم عرصہ سپیسلائیک کیہا جاندا اے، جسدا مطلب اے کہ دو واقعے وقت نالوں سپیس راہیں زیادہ نکھڑویاں ہن۔ دوجے شبداں وچ، دو واقعے درمیان سپیسٹائیم عرصہ پرکاش دی سپیڈ اتے رفتار شیل کسے چیز دی دنیا ریکھا اتے زیرو ہندا اے۔ اجیاے عرصے نوں لائیٹلائیک جاں نلّ کیہا جاندا اے۔ کسے دور واقع تارے توں ساڈی اکھ وچ پہنچے اک پھوٹون دی بالکل عمر نہیں بیتی ہندی، بھاویں اسدے لانگھے وچ اسنے (ساڈے نظریہ توں) سالاں بتائے ہندے ہن۔

صرف اکو سپیس اتے اکو ٹائم نردیشانک والا اک سپیسٹائیم چتر وشیستور تے واہیا جاندا اے۔ چتر 2‑1 اکو گھٹنا توں پیدا ہو راے اتے الٹیاں سمتاں وچ جا راے دو پھوٹوناں A اتے B دیاں ورلڈ لائیناں (یانِ کہ، سپیسٹائیم وچ رستے) سمجھاؤندا اک سپیسٹائیم چتر پیش کردا اے۔ اسدے نال نال، C لائن، پرکاش دی سپیڈ توں دھیمی رفتار نال سفر کردی کسے چیز دی دنیا ریکھا نوں سمجھاؤدی اے۔ ورٹیکل ٹائم نردیشانک ${\textrm {c}}$ ولوں اسطراں سکیلبدھّ کیتا گیا اے تاں جو اسدیاں اوہی یونٹاں ہون (میٹراں وچ) جو ہوریزونٹل سپیس نردیشانک دیاں ہن۔ کیونکہ پھوٹون پرکاش دی سپیڈ نال سفر کردے ہن، اسلئی ایہناں دیاں دنیا ریکھاواں دی ڈھلان 1 دی ہندی اے۔ دوجے شبداں وچ، کسے پھوٹون ولوں سفر کیتا گیا کھبے جاں سجے پاسے ول دا ہریک میٹر، تقریباً وقت دے 3.3 نینوسکنٹ لیندا اے۔

نامکرن اتے نوٹ: رلیٹیوٹی ساہت اندر ورتوں وچ دو چنہ پرمپراواں ہن:

s^{2}=({\textrm {c}}t)^{2}-x^{2}-y^{2}-z^{2}

اتے

s^{2}=-({\textrm {c}}t)^{2}+x^{2}+y^{2}+z^{2}

ایہہ چنہ پرمپراواں میٹرک سگنیچراں (+ − − −) اتے (− + + +)۔ نال جڑیاں ہن۔ ٹائم نردیشانک نوں پہلے نالوں اخیرلے ستھان تے رکھن دا چھوٹا جیہا بدلاؤ وی موجود اے۔ مطالعہ دے کھیتر اندر دوویں پرمپراواں وڈے پدھر تے ورتیاں جاندیاں رہیاں ہن۔ جان-پچھان ول پرتو

ریپھرینس فریماں

وکھریاں ریپھرینس فریماں اندر ساپیکھک طور تے رفتار شیل اؤبزروراں ولوں لئے گئے ناپاں دی تلنا کرن ویلے، کسے معیاری بنتر وچ فریماں سمیت کم کرنا فائدہ مند رہندا اے۔ چتر۔ 2‑2 وچ، دو گیلیلیئن ریپھرینس فریماں (یانِ کہ، پرمپرک 3-سپیس فریماں) نوں ساپیکھک رفتار وچ دکھایا گیا اے۔ فریم S پہلے اؤبزرور O نال متعلق اے، اتیپھریم S’ (جسنوں "S پرائیم" اچاریا جاندا اے) دوجے اؤبزرور O′ نال واسطہ رکھدی اے۔

فریم S دے x، y، z دھرے، فریم S’ دے متعلق پرائیم کیتے گئے دھریاں پرتِ بروبرابر رکھے گئے ہن۔
فریم S′، فریم S دی x-سمت ول اک ستھر ولوسٹی v نال رفتار کردی اے جویں فریم S وچ ناپی گئی ہندی اے۔
فریماں S اتے S′ دے ارجن ادوں مل جاندے ہن جدوں فریم S واسطے ٹائم t = 0 ہندا اے اتے فریم S’ واسطے t′ = 0 ہندا اے۔^[۲۳]^:107

چتر۔ 2‑3a, چتر۔ 2‑2 نوں اک وکھری سمت وچ پھیر توں واہندا اے۔ چتر۔ 2‑3b اؤبزرور O دے نظریہ توں اک سپیسٹائیم ڈائگرام نوں سمجھاؤندا اے۔ کیونکہ S اتے S’ معیاری بنتر وچ ہندیاں ہن، اسلئی ایہناں دے مول نقطہ وقتاں t = 0 (فریم S وچ) اتے t′ = 0 (فریم S’ وچ) اتے آپس وچ ملدے ہن۔ ct′ دھرا فریم S’ وچ واقعے راہیں گزردا اے جسدا x′ = 0 ہندا اے۔ پر x′ = 0 والے نقطہ ولوسٹی v نال فریم S دی x-سمت وچ رفتار کر راے ہندے ہن، تاں جو ایہہ زیرو توں علاوہ کسے ہور وقت اتے ct دھرے اتے آپس وچ نہ ملن۔ اسلئی، ct′ دھرے نوں ہیٹھاں لکھے اینگل θ ولوں ct دھرے توں موڑ دتا جاندا اے؛

\tan \ \theta =v/c.

x′ دھرا وی x دھرے توں گھما دتا جاندا اے۔ اس موڑ دے کین نوں مقرر کرن واسطے، اسیں پھیر توں یاد کردے ہاں کہ کسے پرکاش دی ترنگ دی دنیا ریکھا دی ڈھلان ہمیشاں ہی ±1. Fig. 2‑3c اؤبزرور O’ دے نظرئیے توں اک سپیسٹائیم چتر پیش کردی اے۔ گھٹنا P, x′ = 0, ct′ = −a اتے کسے پرکاش ترنگ دا نکاس پرسعنصر کردی اے۔ ترنگ، پرکاش دے سومے (گھٹنا Q) توں کسے دوری a جنی دور ستھر کسے درپن توں پرورعنصر ہندی اے، اتے پرکاش دے سومے ول x′ = 0, ct′ = a (گھٹنا R) اتے پرط جاندی اے۔

ایہی واقعے P, Q, R چتر۔ 2‑3b وچ اؤبزرور O دی فریم اندر واہیاں گئیاں ہن۔ پرکاش دے رستیاں دیاں ڈھلاناں = 1 and −1 ہن تاں جو ΔPQR اک سمکون والی تکون رچدی اے۔ کیونکہ OP = OQ = OR, اسلئی x′ اتے x درمیان کون ضرور ہی θ ہونا چاہیدا اے۔^[۲۳]^:113–118

جدونکھ ریسٹ فریم اجیاے سپیس اتے ٹائم والے دھرے رکھدی اے جو سمکوناں تے ملدے ہن، تاں رفتار شیل فریم نوں اک اکیوٹ اینگل اتے ملن والے دھریاں نال واہیا جاندا اے۔ فریماں اصل وچ اک-سامان ہی ہندیاں ہن۔ اسمروپیؤ دا کارن اس گل وچ نہ روکی جا سکن والی توڑ-مروڑ ہندا اے کہ سپیسٹائیم نردیشانک کسے کارٹیزیئن پلین اتے کویں میپ کیتا جا سکدا اے، اتے اوس انداز توں زیادہ طاقتوار نہیں منیا جانا چاہیدا، جس وچ، دھرتی دی اک مرکیٹر پروجیکشن اتے میپ کیتے جا سکدے ہون، پولاں (گرینلینڈ اتے انٹارکٹکا) نزدیک دھرتی دے پنجاں دے ساپیکھک اکار بھو-مدھ-ریکھا نیڑے دھرتی پنجاں دی تلنا وچ اچے طور تے بھاری (ودھے) ہندے ہن۔ جان-پچھان ول پرتو

لائیٹ کون

چتر۔ 2-4 وچ، گھٹنا O کسے سپیسٹائیم چتر دے مول نقطہ تے اے، اتے دو ترچھیاں ریکھاواں مول گھٹنا دے حوالہ وچ زیرو سپیسٹائیم عرصہ رکھن والیاں ساریاں واقعے پرسعنصر کردیاں ہن۔ ایہہ دو ریکھاواں اوہ چیز رچدیاں ہن جسنوں گھٹنا O دی لائیٹ کون کیہا جاندا اے، کیونکہ اک دوجی سپیشیئل ڈائمینشن (چتر۔ 2‑5) جوڑن نال ایہہ دکھّ بن جاندی اے کہ دوویں سمکون چکراکار کوناں اپنے اپائیساں O اتے ملدیاں ہن۔ اک کون مستقبل (t>0) ول پھیلدی اے، تے دوجی کون بھوتدور (t<0) ول جاندی اے۔

اک پرکاش (دوہری) کون سپیسٹائیم نوں اسدے اپیکس دے حوالہ وچ وکھرے کھیتراں وچ وبھاجت کردی اے۔ مستقبل لائیٹ کون دا اندرونی حصہ اوہناں ساریاں واقعے دا بنیا ہندا اے جو لائیٹسپیڈ اتے اوہناں دے سپیشیئل ڈسٹینس نوں پار کرن واسطے لازمی وقت نالوں ودھ ٹائم (امستقل دوری) راہیں اپیکس توں وکھریاں ہندیاں ہن؛ ایہہ واقعے گھٹنا O دے ٹائیملائیک مستقبل رچدیاں ہن۔ اسیتراں، بھوتدور لائیٹ کون دیاں اندرونی واقعے ٹائیملائیک بھوتدور ولوں رچیاں جاندیاں ہن۔ اسلئی ٹائیملائیک ارسیاں وچ Δct، Δx توں زیادہ وڈا ہندا اے، جو ٹائیملائیک ارسیاں نوں پوزیٹو بنا دندا اے۔ لائیٹکون دا باہری کھیتر اجہیاں واقعے دا رچیا ہندا اے جو گھٹنا O توں کسے دتے ہوئے ویلے وچ پرکاش دی سپیڈ اتے پار کیتی جان والی سپیس توں زیادہ سپیس راہیں وکھریاں ہندیاں ہن۔ ایہہ واقعے گھٹنا O دا سپیسلائیک کھیتر کیہا جان والا کھیتر رچدیاں ہن، جو چتر۔ 2‑4. وچ “ہور سبھ باقی کسے جگہ” ولوں درسایا جاندا اے۔ خود لائیٹ کون اتے واقعے نوں O توں لائیٹلائیک (جاں “نلّ سیپریٹڈ”) کیہا جاندا اے۔ سپیسٹائیم عرصے دی استحکام صدقہ، سارے اؤبزرور (نریکھک) کسے دتے ہوئی گھٹنا نوں اکو جہی لائیٹ کون حاصل کرنگے، اتے اس کرکے سپیسٹائیم دی اس ونڈ اتے سہمت ہونگے ۔^[۱۴]^:220 لائیٹ کون کارناتمکتا دی دھارنا اندر اک لازمی کردار نبھاؤندی اے۔ O دے پوزیشن اتے ویلے توں D (چتر۔ 2‑4) دے پوزیشن اتے ویلے تک لائیٹ-سپیڈ-توں-دھیمی رفتار نال کسے اشارہ ولوں سفر کرنی ممکن اے۔ اس کرکے گھٹنا O واسطے گھٹنا D اتے اک کارناتمک اثر کرنا ممکن ہو جاندا اے۔ مستقبل دی لائیٹ کون ساریاں اجہیاں واقعے رکھدی اے جو O راہیں کارناتمک طور تے اثر پوا سکدیاں ہن۔ اسے طرحاں، A دی پوزیشن اتے ویلے توں O دے پوزیشن اتے ویلے تک کسے سگنل ولوں پرکاش دی سپیڈ توں گھٹ سپیڈ تے سفر کرنا ممکن اے۔ بھوتدور لائیٹ کون O اتے اک کارناتمک اثر پا سکن والیاں سبھ واقعے دی بندی اے۔ اسدی تلنا وچ، ایہہ مندے ہوئے کہ سگنل پرکاش دی سپیڈ توں تیز سفر نہیں کر سکدے، کوئی وی گھٹنا، جویں اداہرن دے طور تے B or C, جو سپیسلائیک کھیتر وچ اے (باقی کسے ستھان تے)، نہ گھٹنا O نوں متاثر کر سکدی اے، اتے نہ ہی گھٹنا O توں اجیہی سگنل نظام اپنا کے متاثر ہو سکدی اے۔ اس مانتا ماتحت، گھٹنا O اتے کسے لائیٹ کون دے سپیسلائیک کھیتر وچ ہندی کسے گھٹنا درمیان کوئی وی کارناتمک تعلق وچ شامل نہیں کیتا جاندا اے۔^[۲۴] جان-پچھان ول پرتو

تتکالینتا دی ساپیکھکتا

سارے اؤبزرور سہمت ہونگے کہ کسے دتی ہوئی گھٹنا واسطے، دتی ہوئی گھٹنا دی مستقبل لائیٹ کون اندر کوئی گھٹنا، دتی ہوئی گھٹنا توں بعد واپردی اے۔ اسیتراں، کسے وی دتی ہوئی گھٹنا واسطے، بھوتدور لائیٹ کون اندر کوئی گھٹنا، دتی ہوئی گھٹنا توں پہلاں واپردی اے۔ ٹائم-لائیک-وکھریاں کیتیاں واقعے واسطے، پہلاں-بادلاں تعلق تبدیل نہیں ہندے، اس گل نال کوئی فرق نہیں پیندا کہ اؤبزرور دی ریپھرینس فریم کہڑی اے، یانِ کہ، اؤبزرور کسے وی طرحاں رفتار کر رہا ہووے۔ ایہہ پرحالت سپیسلائیک-وکھریانک کیتیاں واقعے واسطے بہت وکھری ہندی اے۔ v = 0 اتے رفتار شیل کسے اؤبزرور دی ریپھرینس فریم توں چتر۔ 2‑4 واہیا گیا اے۔ اس ریپھرینس فریم توں، گھٹنا C, گھٹنا O, توں بعد واپردی اے اتے گھٹنا B, گھٹنا O توں پہلاں واپردی دیکھی جاندی اے۔ کسے وکھری ریپھرینس فریم توں، ایہناں غیر-کارناتمک-سبندھتتمک واقعے دا کرم الٹ ہو سکدا اے۔ خاص کرکے، ایہہ نوٹ کیتا جاندا اے کہ جیکر دو واقعے کسے خاص ریپھرینس فریم اندر اوس ویلے دے ہندیاں ہون، تاں اوہ لازمی طور تے، کسے سپیسلائیک عرصے ولوں وکھریاں ہندیاں ہن اتے اسطراں غیر-کارناتمک طور تے متعلق ہندیاں ہن۔ معائنہ کہ تتکالینتا خالص نہیں ہندی، سگوں اؤبزرور دی ریپھرینس فریم اتے انحصار کردی اے، نوں تتکالینتا دی رلیٹیوٹی کیہا جاندا اے۔^[۲۵]

چتر۔ 2-6 تتکالینتا دی رلیٹیوٹی دے تجزیہ اندر سپیسٹائیم چتراں دی ورتوں سمجھاؤندا اے۔ سپیسٹائیم اندرلیاں واقعے انویریئنٹ ہندیاں ہن، پر “کو-آرڈینیٹ فریماں” بدل جاندیاں ہن جویں چتر۔ 2‑3 واسطے اپر درسایا گیا اے۔ تنے واقعے (A, B, C)، v = 0 اتے رفتار شیل کسے اؤبزرور دی ریفرینس فریم توں اوس ویلے دے ہندیاں ہن۔ v = 0.3 c اتے رفتار شیل کسے اؤبزرور دی ریفرینس فریم توں، ایہہ واقعے، کرم v = 0.3 c وچ واپردیاں دسدیاں ہن۔ v = −0.5 c اتے رفتار شیل کسے اؤبزرور دی ریفرینس فریم توں، ایہناں واقعے دے واپردے دسن دا کرم A, B, C ہندا اے۔ چٹی ریکھا اؤبزرور دے مستقبل ول اؤبزرور دے پاسٹ توں رفتار شیل ہندی ہوئی “تتکالینتا دی ستہِ” نوں اس اتے روشن ہندیاں پرسعنصر کردی اے۔ بھورا کھیتر اؤبزرور دی لائیٹ کون ہندی اے، جو ستھر (انویریئنٹ) رہندا اے۔

اک سپیسلائیک سپیسٹائیم عرصہ انا ہی ڈسٹینس دندا اے جنا کوئی اؤبزرور ناپیگا جیکر واقعے نوں اؤبزرور پرتِ اوس ویلے دے ناپیا جاوے۔ اسطراں کوئی سپیسلائیک سپیسٹائیم عرصہ “پروپر ڈسٹینس”، یانِ کہ، خالص دوری = ${\textstyle {\sqrt {-s^{2}}}.}$ دا اک ناپ مہیا کرواؤندا اے۔ اسیتراں، اک ٹائیملائیک سپیسٹائیم عرصہ اونا ہی ویلے دا ناپ دندا اے جنا کسے دتی ہوئی دنیا ریکھا دے نال نال رفتار شیل کوئی کلوک ودھدی جاں گھٹدی ہوئی ٹکّ کردا ہویا پرسعنصر کریگا۔ اسطراں کوئی ٹائیملائیک سپر عرصہ پروپر ٹائم = ${\textstyle {\sqrt {s^{2}}}}$ دا اک ناپ مہیا کرواؤندا اے۔^[۱۴]^:220–221 جان-پچھان ول پرتو

انویریئنٹ ہائیپربولا

عام یکلڈن سپیس اندر، کسے مول نقطہ توں برابر دوری تے واقع نقطہآں دا سیٹ، کوئی چکر (دو ایاماں وچ)، جاں کوئی سپھیئر (تنّ-ایاماں وچ) رچدا اے۔ منکووسکی سپیسٹائیم وچ، مول نقطہ توں کسے ستھر سپیسٹائیم عرصے اتے نقطہ، ہیٹھاں لکھی اکئیشن ولوں دتی جاندی اک کرو (وقر) رچدے ہن؛

c^{2}t^{2}-x^{2}={\text{some constant}}

اپرلی اداہرن اک x–ct سپیسٹائیم ڈائگرام اندر کسے ہائیپربولے دی اکئیشن اے، جسنوں انویریئنٹ ہائیپربولا کیہا جاندا اے۔ چتر۔ 2-7a وچ، گلابی رنگ والا ہائیپربولا مول نقطہ توں برابر سپیسلائیک وکھریویں والیاں واقعے نوں جوڑدا اے، جدونکھ ہرے رنگا والے ہائیپربولے مول نقطہ توں اک سامان ٹائیملائیک وکھریویں والیاں واقعے نوں جوڑدے ہن۔

نامکرن بارے نوٹ: گلابی ہائیپربولے، جو x دھرے نوں پار کردے ہن، ٹائیملائیک (سپیلائیک نہیں) ہائیپربولے کاے جاندے ہن کیونکہ ایہہ ہائیپربولے اوہ اصلی رستے پرسعنصر کردے ہن جہناں نوں سپیسٹائیم اندر کناں نوں پرویگت کرکے کٹیا جا سکدا اے۔ دوجے پاسے، ہرے ہائیپربولے، جو ct دھرا پار کردے ہن، سپیسلائیک ہائیپربولے کاے جاندے ہن کیونکہ ہائیپربولیاں دے نال نال دی سمت والے سارے عرصے سپیسلائیک عرصے ہندے ہن۔

چتر۔ 2‑7b دکھاؤندا اے کہ جدوں سپیس دی کسے وادھو ڈائمینشن اندر دیکھیا جاندا اے، تاں ٹائیملائیک انویریئنٹ ہائیپربولے اک شیٹ دے ہائیپربولوآئڈ رچدے ہن، جدونکھ سپیسلائیک انویریئنٹ ہائیپربولے دو شیٹاں دے ہائیپربولوآئڈ رچدے ہن۔ جان-پچھان ول پرتو

ٹائم ڈلیشن اتے لینتھ کنٹریکشن

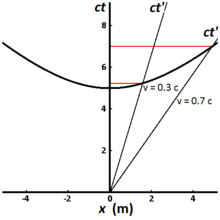
چتر۔ 2-8 اوہناں ساریاں واقعے واسطے انویریئنٹ ہائیپربولے سمجھاؤندا اے جہناں اتے مول نقطہ توں 5 میٹر (تقریباً ۱.67×10^−۸ s) دے پروپر ٹائم وچ پہنچیا جا سکدا اے۔ وکھریاں دنیا ریکھاواں وکھریاں سپیڈاں اتے رفتار شیل کلوک پرسعنصر کردیاں ہن۔ اؤبزرور پرتِ رکے ہوئے (سٹیشنری) کلوک دی دنیا ریکھا ورٹیکل (کھڑویں) ہندی اے، اتے اؤبزرور راہیں ناپیا گیا بیتیا سماں پروپر ویلے جنا ہی ہندا اے۔

0.3c اتے رفتار شیل کسے کلوک واسطے، اؤبزرور راہیں ناپیا جان والا بیتیا سماں 5.24 میٹر (۱.75×10^−۸ s) وچ ملدا اے، جدونکھ 0.7c اتے رفتار کردے کسے کلوک لئی، اؤبزرور راہیں ناپیا گیا بیتیا وقت 7.00 میٹر (۲.34×10^−۸ s) ملدا اے۔ ایہہ ٹائم ڈلیشن نامک ورتارا سمجھاؤندا اے۔ تیز سفر کرن والے کلوک پروپر ویلے دی اڈی ہی مقدار نوں ٹکّ کرن واسطے (اؤبزرور فریم وچ) زیادہ لمبا سماں لیندے ہن، اتے اوہ x–دھرے دی سمت وچ ٹائم ڈلیشن توں بغیر سفر کیتی جان والی دوری توں ہور ودھ دوری سفر کردے ہن۔^[۱۴]^:220–221 وکھریاں انرشیئل ریپھرینس فریماں اندرلے دو اؤبزروراں راہیں ناپی گئی سماں دیری پرسپرک ہندی اے۔ جیکر اؤبزرور O اپنی فریم اندر اؤبزرور O’ دے کلوکاں نوں دھیما چلدا ناپدا اے، تاں اؤبزرور O’ اپنی واری وچ اؤبزرور O دے کلوکاں نوں دھیما دوڑدے ناپیگا۔

لمبائی سنگڑنا (لینتھ کنٹریکشن)، دیری (ڈیلیسن) دی طرحاں، تتکالینتا دی رلیٹیوٹی دا اک پرگٹائ اے۔ لمبائی دا ناپ اجہیاں دو واقعے درمیان سپیسٹائیم عرصے دے ناپ دی منگ کردا اے جو اک دی ریپھرینس فریم وچ اوس ویلے دے ہون۔ پر اوہ واقعے جو اک دی ریپھرینس فریم وچ اوس ویلے دے ہندیاں ہن، سرو عام طور تے، ریفرینس دیاں ہور فریماں توں اوس ویلے دے نہیں ہندیاں ہن۔

چتر۔ 2-9 اک 1 m روڈ دی رفتار سمجھاؤندا اے جو 0.5 c اتے x دھرے دے نال نال سفر کر رہی اے۔ نیلے پٹے دے کنارے روڈ دے دوویں انتلے-سریاں دیاں دنیا ریکھاواں پرسعنصر کردے ہن۔ انویریئنٹ ہائیپربولا 1 m دے کسے سپیسلائیک عرصے ولوں مول نقطہ توں وکھریاں ہوئیاں واقعے سمجھاؤندا اے۔ سرے O اتے B جدوں سانچہ:′ = 0 توں ناپے جاندے ہن، فریم S’ وچ اوس ویلے دے واقعے ہن۔ پر فریم S اندرلے کسے اؤبزرور لئی، واقعے O اتے B اوس ویلے دے نہیں ہن۔ لمبائی ناپن واسطے، فریم S دا اؤبزرور روڈ دے سریاں نوں x-دھرے دی سمت وچ اپنیاں دنیا ریکھاواں اتے سٹے گئے طور تے ناپدا اے۔ روڈ دی ورلڈ-شیٹڈ دی x-دھرے اتے پروجیکشن اگلے پاسے توں گھٹی ہوئی لمبائی OC پیدا کردی اے۔^[۲۳]^:125

(نہ دکھائی گئی) A راہیں اک کھڑویں (ورٹیکل) ریکھا ڈرائینگ جو x-دھرے نوں کٹے ثابت کردی اے کہ، بھاویں OB دی طرحاں، اؤبزرور O دے نزریئے توں اگے توں گھٹ جاندی اے، اسیتراں OA وی اؤبزرور O’ دے نظرئیے توں اگے توں گھٹ جاندی اے۔ جویں ہریک اؤبزرور ہوراں دے کلوک نوں دھیما چلدا ناپدا اے، اویں ہی ہریک اؤبزرور ہوراں دے پیمانیاں نوں سنگڑے ہوئے ناپدا اے۔

پرسپر سماں دیری اتے ٹون پہیلی

پرسپر سماں دیری

پرسپر سماں دیری اتے لمبائی سنگڑنا فزکس دے شروعاتی جگیاسوآں نوں سوے-ورودھی-دھارناواں دے طور تے لگدے تجربہ ہندے ہن۔ چنتا ایہہ ہندی اے کہ جیکر اؤبزرور A, اؤبزرور B دے کلوکاں نوں دھیما دوڑدا ناپدا اے، تاں آسان طور تے اسدا کارن A دے ساپیکھک سپیڈ v اتے B دا رفتار کرنا ہندا اے، پھیر رلٹیوٹی دا اصول منگ کردا اے کہ اؤبزرور B وی اسیتراں A دے کلوکاں نوں دھیما چلدا ناپے ۔ ایہہ اک اہم سوال اے جو سپیشل رلیٹیوٹی پرتِ سمجھ دے دھر تک جاندا اے۔"^[۱۴]^:198

بنیادی طور تے، A اتے B دو وکھرے ناپ لے راے ہندے ہن۔

B دے کلوکاں وچوں کسے اک کلوک دی ہو رہی ٹکّ-ٹکّ دی در نوں ناپن دے چکر وچ، A نوں ضرور ہی اپنے دو کلوک ورتنے چاہیدے ہن، پہلا اوہ سماں درج کریگا جتھے B دا کلوک ”B دی پہلی لوکیشن نوں” پہلی وار ٹکّ کردا اے، اتے دوجا کلوک، اوہ سماں ریکارڈ کریگا جتھے B دا کلوک ”B دی اگلی لوکیشن اتے” اسدی دوجی ٹکّ کڈھدا اے۔ اؤبزرور A نوں دو کلوکاں دی ضرورت پیندی اے کیونکہ B رفتار کر رہا ہندا اے، اس لئی گنتی دے کل تن کلوکاں نوں ناپ وچ سامل کرنا پیندا اے۔ A دے دوویں کلوک A دی فریم اندر سنکرونائز کیتے ہونے چاہیدے ہن۔ اسدے الٹ، B دے دوویں کلوک اسدی فریم وچ A دے کلوکاں دی اوتھے ٹکّ کرن دی لوکیشن درج کرن والی جگہ سنکرونائیز کیتے ہونے منگدے ہن جتھے A دے کلوک اپنے ٹکّ کڈھدے ہن۔ اسطراں، A اتے B ہریک ہی تن کلوکاں دے وکھرے سیٹاں نال اپنے اپنے ناپ لے راے ہندے ہن۔ کیونکہ ایہہ اکو جاے کلوکاں نال اکو جیہا ناپ نہیں لے راے ہندے، اسلئی اجیہی کوئی جنمجات ضرورت نہیں ہندی کہ لئے گئے ناپ اسطراں الٹے طور تے ”انوکول” ہونگے کہ، جیکر اک اؤبزرور دوجے دے کلوک نوں دھیما دوڑدا ناپے، تاں دوجا اؤبزرور پہلے اؤبزرور دے کلوک نوں تیز چلدا ہی ناپیگا۔^[۱۴]^:198–199

پرسپر لمبائی سنگڑن دے حوالہ وچ، چتر۔ 2‑9 سمجھاؤندا اے کہ پرائیم کیتیاں ہوئیاں اتے غیر-پرائیم (پرائیم نہ) کیتیاں ہوئیاں فریماں، کسے ہائیپربولک اینگل ولوں پرسپر گھمائیاں ہویاں ہندیاں ہن (جو یکلڈن جیؤمیٹری (جیؤمیٹری) اندر عام کوناں دے تلّ اے)۔^{[note ۶]} اس روٹیشن کارن، کسے پرائیم کیتی میٹر-سٹکّ دی، پرائیم نہ کیتے x-درے اتے پروجیکشن، اگے توں گھٹ جاندی اے، جدونکھ اسے طرحاں، کسے پرائیم-نہ-کیتیئیم میٹر-سٹکّ دی، پرائیم کیتے x’-دھرے اتے سٹی گئی پروجیکشن وی اگلے پاسیوں گھٹ جاندی اے۔

چتر۔ 2-10 پرسپر سماں دیری بابت پچھلی چرچہ تے زور دندا اے۔ اس چتر وچ، واقعے A اتے C, گھٹنا O توں اک سامان ٹائیملائیک ارسیاں ولوں وکھریاں ہندیاں ہن۔ پرائیم-نہ-کیتیئیم گئی فریم توں، واقعے A اتے B اوس ویلے دے ہون دی طرحاں ناپیاں جاندیاں ہن، پر پرائیم کیتے گئے اؤبزرور نالوں پرائیم-نہ-کیتے-گئے-اؤبزرور لئی زیادہ وقت بیتیا ہندا اے۔ پرائیم کیتی گئی فریم توں، واقعے C اتے D نوں اوس ویلے دے دی طرحاں ہندیاں ناپیا جاندا اے، پر پرائیم نہ کیتے گئے اؤبزرور نالوں پرائیم-کیتے-گئے-اؤبزرور لئی زیادہ وقت بیتیا ہندا اے۔ ہریک اؤبزرور نے دوجے اؤبزرور دے کلوکاں نوں دھیما چلدا ناپیا ہندا اے۔^[۲۳]^:124

کرپا کرکے شبد ناپ دی مہتوپورنتا ول دھیان دیو ۔ کسے اؤبزرور دی رفتار دی حالت کسے اؤبزرو کیتی گئی چیز نوں متاثر نہیں کر سکدی، پر ایہہ چیز پرتِ اؤبزرور دیاں اؤبزرویشناں (نریکھناں) اتے اثر پا سکدی اے۔

چتر۔ 2-10 وچ، x-دھرے دے بروبرابر واہی گئی ہریک ریکھا پرائیم-نہ-کیتیئیم گئے اؤبزرور واسطے تتکالینتا دی اک ریکھا نوں پرسعنصر کردی اے۔ اوس ریکھا اتے ساریاں واقعے دی ct دا ملّ اکو جیہا رہندا اے۔ اسیتراں، سانچہ:′ دھرے پرتِ بروبرابر واہی گئی ریکھا پرائیم کیتے گئے اؤبزرور لئی تتکالینتا دی اک ریکھا پرسعنصر کردی اے۔ اوس ریکھا اتے دیاں ساریاں واقعے سانچہ:′ دا اکو جیہا سماں-ملّ رکھدیاں ہن۔

ٹون پیراڈوکس

سپیشل رلیٹیوٹی پرتِ مڈھلی جان-پچھان اکثر گیلیلیئن رلیٹیوٹی اتے سپیشل رلیٹیوٹی درمیان فرق نوں کلپت کیتے پیراڈوکساں دی اک لڑی پردرشت کرن راہیں سمجھاؤندی اے۔ ساریاں پہیلیاں، دراصل، اصلی طور تے، صرف گلت-پردرشت جاں گلت-سمجھیاں گئیاں سمسیاواں ہن، جو پرکاش دی سپیڈ دے تلنا یوگ ولوسٹیآں پرتِ ساڈی اگیانتا دا نتیجہ ہن۔ علاج سپیشل رلیٹیوٹی وچ بہت ساریاں سمسیاواں نوں حل کرن وچ اے اتے اسدیاں سمجھ-ورتکنیک بھوکھبانیاں کاے جان والے اندازےآں توں جانو ہونا اے۔ سپیسٹائیم دے مطالعہ پرتِ جیؤمیٹری نظریہ نوں اک اجوکی سہج-سمجھج ترقی یافتہ کرن دا سبھ توں چنگا طریقہ منیا گیا اے۔^[۲۶]

ٹون پیراڈوکس اکو جاے جڑواں بھراواں (ٹوناں) والا اک سوچ استعمال اے، جہناں وچوں اک کسے اچّ-سپیڈ روکٹ وچ بیٹھ کے سپیس وچ اک سفر کردا اے، گھر واپس پرتن تے کھوجدا اے کہ دھرتی تے رہن والا اسدا جڑواں بھرا استوں (عمر وچ) زیادہ عمر والا ہو گیا اے۔ ایہہ نتیجہ بجھارت بھریا دسدا اے کیونکہ ہریک ٹون دوجے ٹون نوں رفتار شیل ہندا معائنہ کردا اے، اتے اس کرکے پہلی نظر وچ، ایہہ دسیگا، کہ ہریک نوں دوجا جنا زیادہ عمر والا ہو گیا پاؤنا چاہیدا اے۔ ٹون پیراڈوکس کسے تیجے کلوک دی ضرورت نوں مکا کے اپر درسائی پرسپر ٹائم دیری (ڈیلیشن) واسطے پشٹیکرن نوں سائیڈ تے کر دندا اے۔^[۱۴]^:207 ہور تاں ہور، ٹون پیراڈوکس کوئی خالص پہیلی نہیں اے کیونکہ سپیشل رلیٹیوٹی دے حوالہ اندر ایہہ اسانی نال سمجھ آ جاندا اے۔

اثر کہ کوئی پہیلی موجود اے، اس غلط فہمی توں مضبوط بنی رہندا اے کہ سپیشل رلیٹیوٹی کی بیان کردی اے۔ سپیشل رلیٹیوٹی ساریاں ریپھرینس فریماں نوں اک سامان اعلان نہیں کردی، صرف انرشیئل فریماں نوں کردی اے۔ رفتار شیل ٹون دی فریم ایکسلریٹنگ وقفےآں دوران انرشیئل نہیں ہندی۔ ہور تاں ہور، ٹوناں درمیان فرق نریکھناتمک طور تے پچھانیوگ ہندا اے: رفتار شیل ٹون نوں گھر واپس پرتنیوگ ہون واسطے اپنے روکٹ نوں اگّ لگاؤن دی ضرورت پیندی اے، جدونکھ گھر-رکے رہن والے ٹون نوں اجیہا نہیں کرنا پیندا۔^[۲۷]

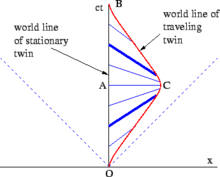
استوں پہلاں کہ اسیں ایہہ سمجھ سکیئے کہ کیوں ایہہ فرق ٹوناں دیاں عمراں وچ اک فرق پاؤندے ہن، گہرے تجزیہ دی ضرورت پیندی اے۔ چتر۔ 2‑11 دے سپیسٹائیم ڈائگرام تے وچار کرو ۔ ایہہ x-دھرے دی سمت وچ سدھے جا راے، اتے ترنت ہی پچھے مڑ راے اک ٹون دا اک آسان معاملہ پرسعنصر کردا اے۔ گھر-ٹھہرے ٹون دے کھڑن دے نقطہ توں، ٹون پہیلی بابت بالکل کجھ وی بجھارت بھریا نہیں اے۔ O توں C تک دی ٹون دی دنیا ریکھا سفر دی سمت وچ ناپے گئے پروپر ٹائم، اتے C توں B تک ناپے گئے پروپر ٹائم دا جوڑ کے O توں A توں B تک دے ناپے گئے گھر-ٹھہرے ٹون والے پروپر ٹائم توں گھٹ رہندا اے۔ رفتار شیل ٹون ولوں محسوس کیتے گئے پروپر ٹائم دی کل مقدار دا حساب لگاؤن واسطے کرو (وقر) دے نال نال متعلق واقعے درمیان پروپر ٹائم نوں جوڑن لئی ہور زیادہ گنجھل دار وکرت رستیاں (کمپلیکس ٹریجیکٹریآں]]) یانِ کہ، پاتھ انٹگرل دی ضرورت پیندی اے۔^[۲۷]

گنجھلدارتاواں پیدا ہو جاندیاں ہن جیکر ٹون پیراڈوکس نوں رفتار شیل ٹون دے نظرئیے توں وشلیشت کیتا جاندا اے۔

اس چرچہ دے باقی حصے لئی، اسیں ویئسّ دا نامکرن طریقہ اپناؤندے ہاں، جو گھر-ٹھہرن والے ٹون نوں ٹیرینس دا نام دندا اے اتے سفر کرن والے ٹون نوں سٹیلا دا نام دندا اے۔^[۲۷]

اسیں پہلاں نوٹ کیتا سی کہ سٹیلا کسے انرشیئل فریم اندر نہیں ہندی ۔ ایہہ حقیقت دتا ہون تے، کدے کدے ایہہ کیہا گیا سی کہ ٹون پیراڈوکس دا مکمل حل جنرل رلیٹیوٹی دی منگ کردا اے۔ ایہہ سچ نہیں اے۔^[۲۷]

اک خالص سپیشل رلیٹیوٹی تجزیہ اسطراں ہو سکدا اے: سٹیلا دی ریسٹ فریم وچ، اوہ سارے دے سارے ٹرپّ لئی رفتار ہین رہندی اے۔ جدوں اوہ مڑن واسطے اپنے راکٹ نوں اگّ لگاؤندی اے، تاں اوہ اک سوڈوپھورس تجربہ کردی اے جو کسے گریویٹیشنل فورس ناکل ملدا جلدا ہندا اے۔^[۲۷] Figs. 2‑6 اتے 2‑11 تتکالینتا دیاں لائیناں (ستہاں) دی دھارنا نوں سمجھاؤندے ہن۔ اؤبزرور دے x-دھرے (xy-پلین) پرتِ بروبرابر ریکھاواں اوہناں واقعے دے سیٹ پرسعنصر کردیاں ہن جو اؤبزرور دی فریم وچ اوس ویلے دے ہندیاں ہن۔ چتر۔ 2‑11 وچ، نیلیاں ریکھاواں ٹیرینس دی دنیا ریکھا اتے واقعے نوں جوڑدیاں ہن جو، سٹیلا دے نظرئیے توں، اسدی دنیا ریکھا اتے واقعے نال اوس ویلے دے ہندیاں ہن۔ (ٹیرینس، بدلے وچ، تتکالینتا دیاں لیٹویاں (ہوریزونٹل) ریکھاواں دے اک سیٹ نوں دیکھیگا) । سٹیلا دی سفر دے باہریہدّ اتے اندرلی حد دے سارے رستے، اوہ اپنے کلوک نالوں ٹیرینس دے کلوکاں نوں دھیما چلدا ناپدی اے۔ پر واپس مڑن ویلے (یانِ کہ، چتر اندرلیاں موٹیاں نیلیاں ریکھاواں درمیان)، تتکالینتا دیاں اسدیاں ریکھاواں دے اینگل وچ اک کھسکاء پیدا ہو جاندا اے، جو ٹیرینس دیی دنیا ریکھا اندرلیاں واقعے دی اک تیز سکپ-اوور نال جڑی ہندی اے جو سٹیلا دے مطابق اسدی اپنی دنیا ریکھا نال اوس ویلے دے ہندی اے۔ اسلئی، اسدے ٹرپ دے انت اتے، سٹیلا کھوجدی اے کہ ٹیرینس اس نالوں زیادہ عمر والا ہو گیا اے۔ ^[۲۷]

بھاویں جنرل رلیٹیوٹی دی لوڑ ٹون پیراڈوکس دے تجزیہ واسطے نہیں پیندی، پھیر وی جنرل رلیٹیوٹی دا برابری اصول موضوع پرتِ کجھ وادھو گہری-سمجھری مہیا کرواؤندا اے۔ اسیں پہلاں ہی نوٹ کیتا سی کہ سٹیلا کسے انرشیئل فریم اندر سٹیشنری نہیں ہندی ۔ سٹیلا دی ریسٹ فریم توں وشلیشت کرن تے، اوہ سارے ٹرپ واسطے رفتار ہین رہندی اے۔ جدوں اوہ بغیر کسے انجن دے آرام نال جا رہی ہندی اے، ادوں اسدی ریسٹ فریم انرشیئل ہندی اے، اتے ٹیرینس دا کلوک دھیما چلدا محسوس ہندا اے۔ پر جدوں اوہ واپس مڑن لئی اپنے راکٹ نوں اگّ لگاؤندی اے، تاں اسدی ریسٹ فریم اک پرویگت فریم بن جاندی اے اتے اوہ اک اجیہا بل تجربہ کردی اے جو اسنوں اسطراں دھکّ رہا ہندا اے جویں اوہ کسے گریویٹیشنل فیلڈ وچ ہووے ۔ ٹیرینس اوس فیلڈ وچ اچا دسیگا اتے گریویٹیشنل ٹائم ڈلیشن کارن، اسدا کلوک تیز بھجدا دسیگا، تاں جو آخری نتیجہ ایہہ راے کہ ٹیرینس دی عمر سٹیلا نالوں زیادہ بیتی ہووے جدوں اوہ واپس اکٹھے ہون ۔^[۲۷] جویں اگلے آؤن والے حصے وقت دا کرویچر وچ چرچہ کیتی جاوے گی، گریویٹیشنل ٹائم ڈلیشن انومانت کر رہیاں اصولی آرگومینٹاں نپانی لئی باہری نہیں ہن۔ گریوٹی دی کوئی وی تھیوری گریویٹیشنل ٹائم ڈلیشن انومانت کریگی جیکر ایہہ برابری اصول دی پالنا کریگی، جس وچ نیوٹن دی تھیوری شامل اے۔^[۱۴]^:16

گریویٹیشن

ایہہ جان-پچھاناتمک حصہ سپیشل رلیٹیوٹی دے سپیسٹائیم اتے مرتکز کیتا گیا اے، کیونکہ اسنوں درساؤنا سبھ توں زیادہ اسان اے۔ منکووسکی سپیسٹائیم فلیٹ ہندی اے، جو گریوٹی نوں شامل نہیں کردی، سبھ جگہ اکسار ہندی اے، اتے اپنے اندر واپردیاں واقعے واسطے اک ستھر پچھوکڑ توں زیادہ ہور کجھ نہیں پیش کردی ۔ گریوٹی دی حاضری وڈا پدھر تے سپیسٹائیم دی وضاحت نوں گنجھل دار کردی اے۔ جنرل رلیٹیوٹی اندر، سپیسٹائیم ہور زیادہ دیر کوئی ستھر پچھوکڑ نہیں رہندا، سگوں عملی طور تے اپنے اندرلے بھوتکی سسٹماں نال پرسپر کریاواں کردا اے۔ مادہ دی حاضری اندر سپیسٹائیم کرواں، ترنگاں دا کمیونیکیشن کر سکدیاں ہن، پرکاش نوں موڑ سکدیاں ہن، اتے ہور بہت سارے ورتارے پردرشت کرن لئی جگہ دے سکدیاں (میزبانی کر سکدیاں) ہن۔^[۱۴]^:221 کجھ اجیاے ورتارے اس لیکھ دے بعد دے حصیاں وچ درسائے گئے ہن۔

سپیسٹائیم دا بنیادی گنت

گیلیلیئن روپانترن

نوٹ: اندرونی وکیپیڈیا-سمپرکاں والے نیویگیشن مثلیاں توں بچن لئی، موبائیل فون ورتونکاراں نوں چاہیدا اے کہ حصہ شارانشاں توں سارے حصیاں نوں جان-پچھان تک واپس پہلاں توں ہی پھیلا لین ۔

اک بنیادی مقصد، ساپیکھک رفتار وچ اؤبزروراں ولوں لئے گئے ناپاں دی تلنا کرن دے یوگ ہونا اے۔ منّ لؤ ساڈے کول فریم S وچ اؤبزرور O اے جو کسے گھٹنا نوں تن کارٹیزیئن نردیشانک اتے اسدے میل کیتے ہوئے کلوکاں (x، y، z، t) (دیکھو چتر۔ 1‑1) دے جال اتے ناپیا گیا وقت حاصل کردا اے۔ اک وکھری فریم S’ اندرلا اک دوجا اؤبزرور اسدے “کو-آرڈینیٹ سسٹم” وچ اوسے گھٹنا اتے میل کیتے ہوئے (سانچہ:′، سانچہ:′، سانچہ:′، سانچہ:′) کلوکاں دے جال نوں ناپدا اے۔ کیونکہ اسیں انرشیئل فریماں نال ورت راے ہندے ہاں، اسلئی کوئی وی اؤبزرور پرویگ (ایکسلریشن) ماتحت نہیں ہندا اے، اتے سمیکرناں دا اک آسان سیٹ سانوں نردیشانکاں (x، y، z، t) نوں نردیشانکاں (سانچہ:′، سانچہ:′، سانچہ:′، سانچہ:′) نال متعلق کرن دی آگیا دندا اے۔ ایہہ دتا ہون تے کہ دو “کو-آرڈینیٹ سسٹم” معیاری رچنا وچ ہن، ایہہ مطلب نکلدا اے کہ ایہہ (x، y، z) نردیشانکاں نال بروبرابر رکھے ہندے ہن اتے t = 0 ہندا اے جدوں سانچہ:′ = 0 ہووے، تاں نردیشانک روپانترن اس طرحاں ہندا اے:^[۲۸]^[۲۹]

x'=x-vt

y'=y

z'=z

t'=t.

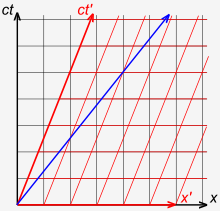
چتر۔ 3-1 سمجھاؤندا اے کہ نیوٹن دی تھیوری اندر، سماں یونیورسل (سنساری) ہندا اے، نہ کہ پرکاش دی ولوسٹی۔^[۳۰]^:36–37 اگے لکھیا سوچ استعمال وچارو: لال تیر پلیٹ فارم دے حوالہ وچ 0.4 c اتے رفتار شیل کوئی ریلگڈی دکھاؤندا اے۔ ریلگڈی اندر، کوئی یاتری گولی شوٹ کردا اے جو ریلگڈی دی فریم اندر 0.4 c دی سپیڈ والی ہندی اے۔ نیل تیر سمجھاؤندا اے کہ ریلگڈی دی پٹڑی اتے کھڑا کوئی انسان گولی دی سپیڈ نوں 0.8 c ناپدا اے۔ ایہہ ساڈیاں مول امیداں مطابق ہی اے۔

ہور سرو عام طور تے، منّ لؤ فریم S دے حوالہ وچ فریم S’ ولوسٹی v نال رفتار کر رہی اے۔ فریم S’ اندر، اؤبزرور O’ کسے چیز نوں ولوسٹی سانچہ:′ نال رفتار شیل ہندی ناپدا اے۔ فریم S دے حوالہ وچ اسدی ولوسٹی u کی ہندی اے؟ کیونکہ x = ut، سانچہ:′ = x − vt، اتے t = سانچہ:′ ہندا اے، اسلئی اسیں سانچہ:′ = ut − vt = (u − v)t = (u − v)سانچہ:′ لکھ سکدے ہاں ۔ ایہہ سانچہ:′ = سانچہ:′/سانچہ:′ ول لجاندا اے اتے انت نوں

u'=u-v

or

u=u'+v,

جو سانجھی-سمجھجھی ولوسٹیاں دے جوڑ واسطے گیلیلیئن نیم اے۔

ولوسٹیاں دی ساپیکھک بنتر

ولوسٹیآں دی بنتر ساپیکھک (ریلیٹیوسٹک) سپیسٹائیم اندر کافی وکھری ہندی اے۔ سمیکرناں دی گنجھلدارتا نوں کجھ گھٹاؤن واسطے، اسیں پرکاش دے ساپیکھک کسے چیز دی سپیڈ دے انوپات واسطے اک سانجھی شورٹہینڈ پیش کردے ہاں،

\beta =v/c

چتر۔ 3-2a اک لال ٹرین (ریلگڈی) دکھاؤندا اے جو v/c = β = s/a دی سپیڈ اتے اگے رفتار شیل ہندی اے۔ ٹرین دے پرائیم کیتے گئے متھے توں، اک یاتری سانچہ:′/c = سانچہ:′ = n/m دی سپیڈ اتے اک گولی شوٹ کردا اے، جتھے دوری (ڈسٹینس) نوں لال سانچہ:′ دھرے دے بروبرابر کسے ریکھا دے نال نال ناپیا جاندا اے نہ کہ کالے x-دھرے دے بروبرابر ۔ جویں نیلے تیر ولوں پرسعنصر کیتا گیا اے، پلیٹ فارم دے ساپیکھک گولی دی مشرت ولوسٹی u کی اے؟ چتر۔ 3‑2b ول اشارہ کیتا جاندا اے:

ولوسٹیاں دے جوڑ واسطے ساپیکھک (ریلیٹیوسٹک) فارمولا جو اپر درسایا گیا اے کئی اہم لچھن دکھاؤندا اے:

جیکر سانچہ:′ اتے v دوویں ہی پرکاش دی سپیڈ نال بہت تھوڑے جاے کمپیئر (تلنا) کیتے جان، تاں گننپھل سانچہ:′/c² بہت سوخم بن جاندا اے، اتے کل نتیجہ ولوسٹیاں دے اس جوڑ لئی گیلیلیئن فارمولے (نیوٹن دے فارمولے) ورگا بن جاندا اے: u = سانچہ:′ + v । گیلیلیئن فارمولا نمن ولوسٹیاں پرتِ لاگوہونیوگ ساپیکھک (ریلیٹیوسٹک) فارمولے دا اک خاص معاملہ اے۔
جیکر سانچہ:′ نوں c برابر سیٹ کیتا جاوے، تاں فارمولا، u = c دندا اے بھاویں v دی شروعاتی قیمت کجھ وی ہووے ۔ پرکاش دی ولوسٹی سارے اؤبزروراں واسطے اکو رہندی اے بھاویں اوہناں دیاں گتیاں پرکاش دا نکاس کرن والے سومے دے ساپیکھک کجھ وی ہون۔^[۳۰]^:49

سماں دیری اتے لمبائی سنگڑنا دوہراء

سماں دیری اتے لمبائی سنگڑن بارے، گناتمک شبداں وچ، اسیں پہلاں ہی چرچہ کر چکے ہاں ۔ ایہناں اثراں واسطے ماتراتمک سمیکرناں حاصل کرنیاں سدھی گل ہی اے۔ چتر۔ 3‑3 اس حصے دے مقصداں لئی دوویں پچھلیاں اینیمیشناں توں لئیاں گئیاں، آسان کیتیاں ہوئیاں اتے پنر-نامبدھّ کیتیاں ہوئیاں انفرادی فریماں رکھن والی مشرت تصویر اے۔

سمیکرناں دی گنجھلدارتا نوں کجھ گھٹاؤن واسطے، اسیں ساہت وچ ct لئی وکھریاں شورٹہینڈ چنہ-دھارناواں دی اک ویرائٹی دیکھدے ہاں؛:

\mathrm {T} =ct

اتے

w=ct

عامَ ہن۔

پرمپرا

c=1.

دی اکثر ورتوں وی دیکھی جاندی اے۔

چتر۔ 3-3a وچ، حصے OA اتے OK اک سامان سپیسٹائیم عرصے پرسعنصر کردے ہن۔ سماں دیری نوں انوپات OB/OK راہیں پرسعنصر کیتا جاندا اے۔ انویریئنٹ ہائیپربولا مساوات $w = سانچہ:Radical$ رکھدا اے جتھے k = OK، اتے لال ریکھا، w = x/β = xc/v مساوات والی رفتار والے کسے کن دی دنیا ریکھا نوں پرسعنصر کردے ہن۔ کجھ الجبرک دخل-اندازی ${\textstyle OB=OK/{\sqrt {1-v^{2}/c^{2}}}}$ پیدا کردی اے۔

طبقہ مول چنہ سمیت والی مساوات رلیٹیوٹی اندر بہت وار دسدی اے، اتے اک بٹا ایہہ مساوات (1/مساوات) نوں لورنٹز پھیکٹر کیہا جاندا اے، جو گریک اکھر گاما $\gamma$ نال درسایا جاندا اے:^[۳۱]

\gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}

اسیں نوٹ کردے ہاں کہ جیکر v، c توں وڈی جاں برابر ہووے، تاں $\gamma$ واسطے مساوات بھوتکی طور تے بے مطلب ہو جاندی اے، جسدا مطلب اے کہ c، قدرت وچ ودھ توں ودھ ممکن سپیڈ اے۔ استوں بعد، اسیں نوٹ کردے ہاں کہ زیرو توں ودھ کسے وی v لئی، لورنٹز پھیکٹر اک توں وڈا ہووےگا، بھاویں کرو دی شکل اجیہی ہندی اے کہ نمن سپیڈاں واسطے، لورنٹز پھیکٹر اک دے مقصد (بہت زیادہ) نیڑے ہندا اے۔

چتر۔ 3-3b وچ، حصے OA اتے OK اک سامان سپیسٹائیم عرصے پرسعنصر کردے ہن۔ لمبائی سنگڑن نوں انوپات OB/OK نال دکھایا جاندا اے۔ انویریئنٹ ہائیپربولے دی مساوات $x = سانچہ:Radical$ ہندی اے، جتھے k = OK، اتے نیلے بینڈ دے کنارے سلوپ (ڈھلان) 1/β = c/v والی رفتار وچ کسے روڈ دے سریاں دیاں دنیا ریکھاواں پرسعنصر کردے ہن۔ گھٹنا A دے نردیشانک ایہہ ہندے ہن؛

(x، w) = (γk، γβk) । کیونکہ A اتے B راہیں سمرد ریکھا دی مساوات w = (x − OB)/β ہندی اے، اسلئی اسیں γβk = (γk − OB)/β اتے؛

OB/OK=\gamma (1-\beta ^{2})={\frac {1}{\gamma }}

حاصل کردے ہاں۔

لورنٹز روپانترن

گیلیلیئن ٹرانسپھورمیشناں اتے ولوسٹیآں دے جوڑ دے اہنا دے اگلے سانجھی-بدھی دے نیم، پلیناں، کاراں اتے گینداں دے ساڈے عام گھٹّ-سپیڈ والے دنیا وچ بہت چنگی طرحاں کم کردے ہن۔ مدھ-1800ویں دہاکے دی شروعات وچ، کویں نہ کویں، سنویدنشیل سائنسی اپکرناتمکتا نے اجہیاں وسنرفتارآں (بیمیلتاواں) کھوجنیاں شروع کر دتیاں سن، جو ولوسٹیآں دے عام جوڑ نال فٹ نہیں بیٹھدیاں سن۔

سپیشل رلیٹیوٹی اندر اک فریم توں کسے دوجی فریم وچ کسے گھٹنا دے نردیشانکاں نوں روپانترت کرن واسطے، اسیں لورنٹز روپانترناں ورتدے ہاں ۔

لورنٹز روپانترناں اندر لورنٹز پھیکٹر دسدا اے:

{\begin{aligned}t'&=\gamma \left(t-{\frac {vx}{c^{2}}}\right)\\x'&=\gamma \left(x-vt\right)\\y'&=y\\z'&=z\end{aligned}}

الٹیاں لورنٹز روپانترناں ایہہ ہندیاں ہن:

{\begin{aligned}t&=\gamma \left(t'+{\frac {vx'}{c^{2}}}\right)\\x&=\gamma \left(x'+vt'\right)\\y&=y'\\z&=z'\end{aligned}}

جدوں v ≪ c ہندی اے، تاں v²/c² اتے vx/c² رقماں زیرو نیڑے پہنچ جاندیاں ہن، اتے لورنٹز روپانترناں گیلیلیئن روپانترناواں دے تقریباً برابر ہو جاندیاں ہن۔

جویں پہلاں وی نوٹ کیتا گیا اے، جدوں اسیں $t'=\gamma (t-vx/c^{2}),$ $x'=\gamma (x-vt)$ اتے ہور اگے اسیتراں لکھدے جاندے ہاں، تاں زیادہتر اکثر ساڈا مطلب اصلی طور تے $\Delta t'=\gamma (\Delta t-v\Delta x/c^{2}),$ $\Delta x'=\gamma (\Delta x-v\Delta t)$ وغیرہ ہندا اے۔ بھاویں، بہادر بندے ہوئے، اسیں لورنٹز روپانترناں نوں ڈیلٹیاں ٹوپولوجی بغیر ہی لکھدے ہاں، پھیر وی ایہہ سمجھ لینا چاہیدا اے کہ x دا مطلب Δx اے، وغیرہ ۔ اسیں، عامطور تے، ہمیشاں ہی واقعے درمیان سپیس اتے ویلے دے انتراں نال واسطہ رکھدے ہاں ۔

نامکرن اتے نوٹ: روپانترناں دے اک سیٹ نوں نورمل لورنٹز روپانترناں کہنا اتے دوجے نوں الٹ روپانترن کہنا گلتوہمی پیدا کردا اے، کیونکہ فریماں درمیان کوئی اندرونی انتر نہیں ہندا ۔ وکھرے ودوان اک جاں دوجے روپانترن سیٹ نوں الٹا سیٹ پکاردے ہن۔ اگے ول دیاں اتے الٹ روپانترناں اک دوجے پرتِ سوخم طور تے متعلق ہندیاں ہن، کیونکہ S فریم صرف اگے ول نوں رفتار شیل ہو سکدی اے جاں سانچہ:′ دے حوالہ وچ الٹ ہو سکدی اے۔ اسلئی، سمیکرناں نوں الٹا دینا آسان طور تے پرائیم کیتے اتے غیر-پرائیم کیتے استھرانکاں نوں اتے v نوں −v نال بدل دینا ہی اے۔^[۳۲]^:71–79

اداہرن: ٹیرینس اتے سٹیلا دھرتی توں منگل سیارہ تک سپیس ریس اتے ہن۔ ٹیرینس شروعاتی ریکھا اتے اک اؤپھیشیئل اے، جدونکھ سٹیلا اک کونٹیسٹنٹ اے۔ t = سانچہ:′ = 0 ویلے اتے، سٹیلا دا سپیش-شپش اوس ویلے دے اک سپیڈ 0.5 c تک پرویگت ہو جاندا اے۔ دھرتی توں منگل سیارہ تک دی دوری 300 پرکاش-سکنٹش (تقریباً ۹۰.0×10^۶ کلومیٹر) اے۔ ٹیرینس سٹیلا نوں پھنش-لائینش کلوک t = 600.00 s تے پار کردا دیکھدا اے۔ پر سٹیلا اپنے شپ-کرونومیٹر اتے ٹائم سانچہ:′ = $\gamma$ (t − vx/c²) = 519.62 s ہندا پاؤندی اے جیوں ہی اوہ پھنش لائن توں گزردی اے، اتے اوہ شروعاتی تے انت-لائن درمیان دوری نوں اپنی فریم وچ 259.81 لائیٹ-سیکنڈ (تقریباً ۷۷.9×10^۶ کلومیٹر) ہندا پاؤندی اے۔ 1)۔

لورنٹز روپانترناں ویونتبند کرنا

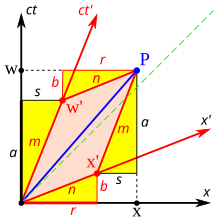
1905 وچ آئینسٹائین دے ارجنل کم توں بعد کئی درزناں لورنٹز ٹرانسپھورمیشناں دیاں ویونتبندیاں رہیاں ہن، جہناں وچوں ہریک دا اپنا خاص پھوکس سی۔ بھاویں آئینسٹائین دی ڈیریویشن پرکاش دی سپیڈ دی انویریئنس (استحکام) اتے مشتمل سی، پھیر وی ہور بھوتکی اصول اجیاے ہن جو شروعاتی نقطےآں پھدے طور تے ورتے جا سکدے ہن۔ انت نوں، ایہہ الٹرنیٹو شروعاتی نقطہ ستھانکتا اصول پچھے چھپیاں وکھریاں سمیکرناں منے جا سکدے ہن، جو بیان کردا اے کہ اک دوجے اتے پائے گئے کناں دے اثر نوں اکدم (اوس ویلے دے) سنچارت نہیں کیتا سکدا۔^[۳۳]

اتھے دتی گئی ڈیریویشن جو چتر۔ 3‑5 وچ دکھائی گئی اے، ولوسٹیاں دے ساپیکھک (ریلیٹیوسٹک) مرکب، ٹائم ڈلیشن، اتے لینتھ کنٹریکشن حصیاں توں پچھلے نتیجیاں دی ورتوں کرکے باعث^[۳۰]^:64–66 دی اک پیش کش اتے مشتمل اے۔ گھٹنا P دے نردیشانک (w، x) ہندے ہن جو کالے ریسٹ سسٹم وچ ہندے ہن اتے نردیشانک (سانچہ:′، سانچہ:′) لال فریم وچ ہن جو ولوسٹی پیرامیٹر β = v/c نال رفتار کردے ہن۔ اسیں سانچہ:′ اتے سانچہ:′ نوں w اتے x دے شبداں وچ کویں مقرر کردے ہاں؟ (جاں کسے ہور طرحاں، بالکل) الٹ لورنٹز روپانترن نوں پہلاں ہی ویونتبند کرنا اسان رہندا اے۔

اسیں اوہ نوٹ کردے ہوئے شروع کردے ہاں کہ لمبائی پھیلاؤ/سنگڑن ورگی کوئی چیز ٹرانسورس سمتاں وچ نہیں ہندی ۔ yسانچہ:' ضرور ہی y برابر ہونی چاہیدی اے اتے سانچہ:′ ضرور ہی z برابر ہونا چاہیدا اے، نہیں تاں چااے کوئی تیز رفتار شیل 1 m گیند کسے 1 m چکراکار سوراخ وچ فٹ ہو سکدی اے کہ نہیں، اؤبزرور اتے انحصار کردا اے۔ رلیٹیوٹی دا پہلا سوے-سدھ اصول بیان کردا اے کہ ساریاں انرشیئل فریماں اک-سامان ہندیاں ہن، اتے ٹرانسورس پھیلاؤ/سنگڑن اس نیم دی النگھنا کردی ہو سکدی اے۔^[۳۲]^:27–28
ڈرائنگ توں، w = a + b اتے x = r + s ।
سمروپ تکوناں ورتدے ہوئے پچھلے نتیجیاں توں، اسیں جاندے ہاں کہ s/a = b/r = v/c = β ।
اسیں جاندے ہاں کہ سماں دیری کارن، a = γسانچہ:′ ।
مساوات (4) نوں s/a = β وچ بھردے ہوئے s = سانچہ:′β ملدا اے۔
لمبائی سنگڑنا اتے سمروپ تکوناں سانوں r = سانچہ:′ اتے b = βr = βγسانچہ:′ دندے ہن۔
s، a، r اتے b واسطے سمیکرناں نوں سٹیپ 2 وچ بھرن تے ترنت ہی ایہہ ملدا اے؛
$w=\gamma w'+\beta \gamma x'$

$x=\gamma x'+\beta \gamma w'$

اپرلیاں اکئیشناں الٹ لورنٹز ٹرانسپھورمیشناں دیاں t اتے x سمیکرناں واسطے بدلویاں سمیکرناں ہن، جویں کہ ct نوں w لئی، سانچہ:′ نوں سانچہ:′ لئی، اتے v/c نوں β واسطے بھرکے دیکھیا جا سکدا اے۔ الٹ روپانترن توں، پھارورڈ روپانترن نوں سانچہ:′ اتے سانچہ:′ واسطے ویونتبند کرکے حل کیتا جا سکدا اے۔ ’‘جان-پچھان ول پرتو’’

لورنٹز ٹرانسپھورمیشناں دی ریکھکتا

لورنٹز ٹرانسپھورمیشناں دی اک گنتک خاصیت رکھدیاں ہن جس نوں لینیئرٹی کیہا جاندا اے، کیونکہ xسانچہ:' اتے tسانچہ:' نوں x اتے t دے اک ریکھک میل دے طور تے، بغیر اچّ پاوراں نوں شامل کیتے حاصل کیتا جا سکدا اے۔ ٹرانسپھورمیشن دی ریکھکتا، سپیسٹائیم دی اک بنیادی خاصیت پرورعنصر کردی اے جو اسیں مون روپ وچ (چپ چاپ) اودوں منّ لیا سی جدوں ڈیریویشن ویونتبند کر راے سی، کہ ریپھرینس انرشیئل فریماں دیاں خاصیتاں لوکیشن اتے ویلے توں آزاد ہندیاں ہن۔ گریوٹی دی غیر-حاضری وچ، سپیسٹائیم سبھ تھاں اکو جیہا لگدا اے۔^[۳۰]^:67 سارے انرشیئل اؤبزرور رفتار دے پرویگت ہون اتے پرویگت نہ ہون پچھے دے کارن اتے سہمت رہنگے۔^[۳۲]^:72–73 کوئی وی اؤبزرور سپیس اتے ویلے دے اپنے ناپ ورت سکدا اے، پر اس بارے کجھ وی خالص نہیں ہندا ۔ کوئی ہور اؤبزرور دیاں پرمپراواں وی اویں ہی کرنگیاں۔^[۱۴]^:190

لینیئرٹی دا اک نتیجہ ایہہ اے کہ جیکر دو لورنٹز ٹرانسپھورمیشناں (روپانترن) لڑیوار (ترتیب وار) لاگوُ (اپلائی) کیتیاں جان، تاں نتیجہ وی اک لورنٹز ٹرانسپھورمیشن ہی ہندا اے۔

اداہرن: ٹیرینس سٹیلا نوں اپنے توں 0.500 c تے دور جاندی نریکھت کردا اے، اتے اوہ اپنے ناپاں نال سٹیلا دے ناپاں نوں متعلق کرن لئی β = 0.500 سمیت لورنٹز ٹرانسپھورمیشناں ورت سکدا اے۔ سٹیلا، اپنی فریم اندر، ارسلا نوں اپنے توں 0.250 c اتے دور جاندی نریکھت کردی اے، اتے اوہ اپنے ناپاں نال ارسلا دے ناپاں نوں متعلق کرن واسطے β = 0.250 سمیت لورنٹز ٹرانسپھورمیشناں ورت سکدی اے۔ ٹرانسپھورمیشناں دی ریکھکتا (لینیئرٹی) اتے ولوسٹیاں دی ساپیکھک (ریلیٹیوسٹک) بناوٹ کرکے، ٹیرینس اپنے ناپاں نال ارسلا دے ناپاں نوں متعلق کرن واسطے β = 0.666 سمیت لورنٹز ٹرانسپھورمیشناں نوں ورت سکدا اے۔

ڈوپلر اثر