سٹرینگ تھیوری
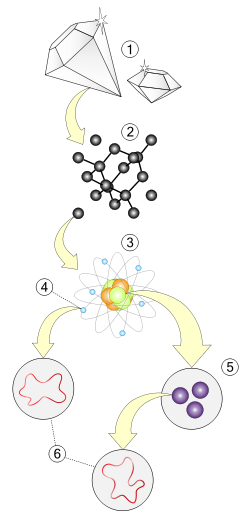
1. وڈا پدھر: مادہ
2. انو پدھر
3. ایٹمی پدھر: پروٹان، نیوٹران اتے الیکٹران
4. سب-ایٹمی پدھر: الیکٹران
5. سب-ایٹمی پدھر: کوارک
6. ڈور-پدھر
فزکس وچّ، سٹرنگ تھیوری (جاں ڈوری اصول) اک اصولی ڈھانچہ ہے جس وچّ پارٹیکل فزکس دے بندو ورگے ایٹماں نوں 1-پساری وستواں وچّ بدل دتا جاندا ہے جہناں نوں سٹرنگ (ڈوریاں) کہندے ہن۔ سٹرنگ تھیوری وچّ، دیکھے گئے مڈھلے ایٹماں دیاں وکھریاں قسماں ایہناں سٹرنگاں دیاں وکھریاں وکھریاں ‘کوانٹم حالتاں’ توں پیدا ہندیاں ہن۔ پارٹیکل فزکس دے سٹینڈرڈ ماڈل وچّ دکھائے کناں توں علاوہ، سٹرنگ تھیوری قدرتی طور تے گوروتا کھچّ نال وی میل کھاندی ہے، جس کارن ہریک چیز دی تھیوری دے یوگ ہے، جو سارے مڈھلے کن اتے مادےدیاں قسماں نوں درساؤن والا اک آتم-نربھر گنتی ماڈل ہے۔ کن بھوتکی وچّ اس دھارنا دے رول توں علاوہ، سٹرنگ تھیوری ہن وڈے پدھر تے اک سدھانتک-شاستر دے روپ وچّ ورتی جاندی ہے، تے اسنے کوانٹم فیلڈ تھیوری تے کوانٹم گریوٹی دے بہت سارے پہلوآں تے روشنی پائی ہے۔
سٹرنگ تھیوری دے سبھ توں پہلے ماڈل وچّ، جس نوں بوسونک سٹرنگ تھیوری کیہا جاندا ہے، صرف بوسون کناں دی شرینی دا سہیوگ کیتا گیا، بے شک ایہہ تھیوری بعد وچّ سپرسٹرنگ تھیوری وچّ وکست ہو گئی، جسنے درسایا کہ بوسون اتے پھرمیؤن کناں درمیان اک سپرسمروپتا (supersymmetry) دا سبندھ ہے۔ سٹرنگ تھیوری نوں وادھو ستھانک ایاماں دی ضرورت پیندی ہے تاں جو اسدا گنت ستھر رہے| سٹرنگ تھیوری توں بنے واستوک بھوتکی ماڈل وچّ، ایہہ وادھو ایام بہت سوکھمتا دے درجے تکّ سنگڑے (compactified) ہندے ہن۔
سٹرنگ تھیوری سبھ توں پہلی وار 1960ویں دہاکے دے اخیر وچّ طاقتور کیندری بل دی تھیوری دے روپ وچّ پڑی گئی جستوں بعد کوانٹم کروموڈئنیمکس تھیوری دے پکھ وچّ چھڈّ دتی گئی| فلسروپ، ایہہ محسوس کیتا گیا کہ سٹرنگ تھیوری دیاں مڈھلیاں وشیشتاواں جو پرمانو بھوتکی تھیوری لئی یوگ نہیں سن اوہ کوانٹم گروتاکرشن تھیوری دے یوگ ہن۔ 1990ویں دہاکے دے مدھ وچّ رلیز ہون توں پہلاں سٹرنگ تھیوری دے 5 ستھر روپ وکست کیتے گئے کہ ایہہ 5 تھیوریاں جوڑ کے اک وکھری 11-ایامی M-تھیوری بنی جسدیاں وکھریاں وکھریاں سیماواں دے روپ وچّ ایہہ 5 قسماں بن سکدیاں سن۔
بہت سارے بھوتک شاستری (جویں، سٹیپھن ہاکنگ، ایڈورڈ وٹن، اتے جوان مالڈسینا) مندے ہن کہ سٹرنگ تھیوری قدرت دے مڈھلے وستھار نوں صحیح کرن ولّ قدم ہے۔ اجیہا اس لئی ہے کیونکہ ایہہ تھیوری کوانٹم پھیلڈ تھیوری اتے جنرل رلیٹوٹی دے ستھائی میل نوں سنبھوَ کردی ہے، کوانٹم گریوٹی دیاں عامَ گہرائییاں جویں ہولوگراپھک سدھانت تے بلیک ہول تھرموڈائنامکس نال وی سہمت ہے، اتے اسنے بہت سارے اندرونی ستھرتا دے گمبھیر ٹیسٹ پاس کیتے ہن۔ خاص کر کے سٹیپھن ہاکنگ مطابق، ‘M- تھیوری ہی برہمنڈ دی سمپورن تھیوری دے قابل ہے۔” ہور بھوتک وگیانی ، جویں رچرڈ پھینمین، روجر پینروس، شیلڈن لی گلاشو، نے سٹرنگ تھیوری دی الوچنا کیتی ہے کیونکہ ایہہ اورجا دے پیمانیاں تے پریوگاں دی بھوکھبانی دی کتھا نہیں اپلبدھ کرواؤندی اتے تے کیہا کہ ایہہ ہریک چیز دی تھیوری دے طور تے اسپھل ہے۔
سٹرنگ تھیوری تتّ-نکھیڑ
سودھو
سٹرنگ تھیوری دا شروعاتی وچار ایہہ ہے ہے کہ پارٹیکل پھجکس دے بندو ورگے کناں نوں سٹرنگ نامک 1-ایامی وستواں وچّ پیش کیتا جا سکدا ہے۔ سٹرنگ تھیوری مطابق، سٹرنگ کئی طریقیاں نال کمپن کر سکدے ہن۔ سٹرنداں دے اردھ ویاس توں ودھ والے ستھاناں تے ، ہریک کمپن دا طریقہ وکھرے قسم دے پونج، چارج اتے ہور گناں والے دے کن نوں رچدا ہے جو سٹرنگ ڈائنیمکس نال ناپے جا سکدے ہن۔ سٹرنگاں دا ٹٹنا تے دوبارہ جڑنا کناں دے پیدا ہون تے گرہن کیتے جان نال سبندھ رکھدا ہے، جو کناں وچکارلی پرسپر کریاواں نوں پیدا کردی ہے۔ سٹرنگاں دے کمپن دے طریقیاں دی اداہرن اک گٹار دی تار دوارا پیدا ہون والیاں کئی وکھریاں سنگیت دیاں دھناں وانگ ہے۔ اس اداہرن وچّ، وکھریاں دھناں وکھرے کناں نال سبندھت ہن۔
سٹرنگ تھیوری وچّ، سٹرنگ دے کمپن دے طریقیاں وچوں اک طریقے دا سبندھ اک پنجہین، سپن-2 کن نال ہے۔ اجیہا کن گریویٹون کیہا جاندا ہے کیونکہ ایہہ اجیہے بل نوں سواری کراؤندا ہے جس وچّ گروتاکرشن دا گن ہندا ہے۔ کیونکہ سٹرنگ تھیوری نوں اک ستھر گنتک کوانٹم مکینکس تھیوری منیا جاندا ہے، اسلئی اس گریویٹون کن دی ہوند دی اوستھا دا مطلب ہے کہ سٹرنگ تھیوری کوانٹم گریوٹی دی تھیوری ہے۔
سٹرنگ تھیوری وچّ دوہے طرحاں دے سٹرنگ شامل ہن۔ جہناں وچّ اک کھلے سٹرنگ ہندے ہن جہناں دے دو وکھرے انتمبندو (سرے) ہندے ہن۔ دوجی طرحاں دے سٹرنگ پورا چکر بناؤندے ہن، یانِ کہ بند سریاں والے ہندے ہن۔ دوویں قسم دے سٹرنگ ذرا وکھرے طریقے نال ورتاؤ کردے ہن، تے وکھری قسم دے کن رچدے ہن۔ جویں، ساریاں سٹرنگ تھیوریاں وچّ بند سٹرنگ گریویٹون طریقے ہن، پر صرف کھلے سریاں والے سٹرنگ ہی پھوٹون نامک کناں نال سبندھ رکھدے ہن۔ کیونکہ اک کھلے سٹرنگ دے دوہے سرے ہمیشہ مل کے جڑ سکدے ہن. تے بند سٹرنگ رچ سکدے ہن، اسلئی ساریاں تھیوریاں وچّ بند سٹرنگ ہندے ہن۔ اک سٹرنگ دی لمبائی پلینک لمبائی برابر ہندی ہے۔ شروعاتی ماڈل وچّ، بوسونک سٹرنگ، نے صرف بوسون کناں دی شرینی دا ہی سہویوگ کیتا| ایہہ ماڈل، گھٹّ اورجاواں تے، اک کوانٹم گریوٹی تھیوری، جس وچّ گیز بوسون جویں پھوٹون وی شامل ہن (جیکر کھلے سرے والے سٹرنگ وی شامل کر لئے جان) دی ویاکھیا کردا ہے۔ پھیر وی، اس ماڈل وچّ سمسیاواں ہن۔ سبھ توں زیادہ مہتوپورن ایہہ ہے کہ تھیوری وچّ مول اتھرتا ہندی ہے، جو نتیجے وجوں اپنے آپ وچّ ہی سپیس سمیں دا رساؤ کردا منی جاندی ہے(گھٹو گھٹّ انشک روپ وچّ)| اسدے نال ہی، جویں اسدا نام درساؤندا ہے کناں دا رنگ-پٹا (سپیکٹرم) صرف بوسناں دا ہی ہے اتے کن جویں پھوٹین ، وطیرے دے خاص گناں دی پالنا کدے ہن، دا ہے۔ موٹے طور تے کہندے ہوئے، بوسن رساؤ دے جنم داتا کن ہن، پر پدارتھ دے نہیں، جو پھرمیؤنز دا بنیا ہندا ہے۔ایہہ جانچ کردے ہوئے کہ کویں سٹرنگ تھیوری پھرمیؤن وی شامل کر سکدی ہے نے سپرسمٹری دی کھوج نوں جنم دتا، جو بوسوناں اتے پھرمیؤناں درمیان گنتک سبندھ ہے۔ پھرمؤن کمپنا سمیت والی تھیوریاں نوں سپرسٹرنگ تھیوریاں کیہا جاندا ہے؛ کئی قسماں درسائیاں گئیاں ہن، پر ہن ساریا M-تھیوری دیاں وکھریاں سیماواں ہون دے روپ وچّ سوچیاں جاندیاں ہن۔
کیونکہ سٹرنگ تھیوری ساریاں مڈھلیاں کریاواں نال میل کھاندی ہے، جس وچّ گریوٹی وی شامل ہے، کئی وگیانیاں نوں امید ہے کہ ایہہ ساڈے برہمنڈ نوں پوری طرحاں درساؤندی ہے تے اس نوں تھیوری آف ایوریتھنگ بنا دندی ہے۔ سٹرنگ تھیوری وچّ تازہ کھوجاں دا اک مکھ منتوَ اجیہی تھیوری دا حلّ لبھنا ہے جو سٹینڈرڈ ماڈل نال نتیجیاں دے روپ وچّ میل کھاوے، چھوٹے برہمنڈی ستھر انک نال میل کھاوے، جس وچّ ڈارک میٹر ہندا ہے تے برہمنڈی مدراسپھیرتی (cosmic inflation) لئی تعریف دے قابل تنتر نال میل کھاوے| ایہہ اجے تکّ اگیات ہے کہ سٹرنگ تھیوری وچّ کوئی اجیہا حلّ ہے، نہ ایہہ پتہ چلیا ہے کہ ایہہ تھیوری وستھار دی چون لئی کنی کو آزادی دی آگیا دندی ہے۔
سٹرنگ تھیوری دیاں چنوتیاں وچوں اک ایہہ ہے کہ ساری تھیوری اجے تکّ سارے ہلاتاں وچّ سنتشٹیدائک پریبھاشا نہیں دے سکی| سٹرنگاں دے کھنڈاؤ زیادہتر سدھے ہی گڑبڑی سدھانت (perturbation theory) دیاں تکنیکاں ورت کے پربھاشت کیتے گئے ہن، پر عامَ طور تے ایہہ اگیات ہے کہ بغیر گڑبڑی نال سٹرنگ تھیوری نوں کویں پربھاشت کیتا جاوے| ایہہ وی سپشٹ نہیں ہے کہ کی کوئی اجیہا سدھانت ہے جاں نہیں جس نال سٹرنگ ‘vacuum state’ (پلاڑ اوستھا ) چندی ہے، جو ساڈے برہمنڈ دے گناں نوں نردھارت کرن والی سپیس ٹائم بنتر ہے۔
سٹرنگ (ڈوری)
سودھو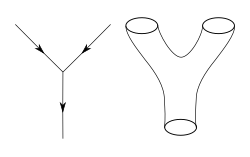
کسے بندو ورگے کن دی گتی درساؤن لئی اک گراف تے اسدا ستھان وقت دے حساب نال درسایا جا سکدا ہے۔ نتیجن تصویر سپیس سمیں وچّ اسد کن دی سنسار-ریکھا درسائیگی| اک ہور برابر طریقے نال، وقت دے گزرن دے نال نال سٹرنگ دی گتی نوں درسایا جا سکدا ہے۔ سٹرنگ، جو اپنے آپ وچّ چھوٹی ریکھا وانگ دسدے ہن، اک 2-پساری ستہ جھاڑدے جاندے ہن جسنوں ورلڈشیٹ (سنساری چادر) کہندے ہن۔ وکھریاں سٹرنگ حالتاں (پھوٹون جاں گریویٹون ورگے وکھرے کناں نوں رچدے ہوئے) اس ستہِ تے ترنگاں وانگ لگدے ہن۔
اک بند سٹرنگ اک چھوٹے لوپ وانگ دسدا ہے، اسلئی اسدی ورلڈشیٹ پائیپ وانگ دسیگی| اک کھلا سٹرنگ دو سریاں والے چھوٹے حصے وانگ دسیگا، اسلئی اسدی ورلڈشیٹ اک پٹی ورگی دسیگی| ہور زیادہ گنتی بھاشا ورتدے ہوئے، ایہہ دوویں رائیمن تل (Riemann surfaces) ہن ، جس وچّ پٹی دی اک حد ہندی ہے پر پائیپ دی حد نہیں ہندی|
سٹرنگ جڑ اتے ٹٹّ سکدے ہن۔ ایہہ اوہناں دی ورڈلشیٹ توں پتہ چلدا ہے، جاں سنکھیپ وچّ کہیئے تاں اوہناں دے سمستھتی (topology) توں پتہ چلدا ہے۔ جویں، جے اک بند سٹرنگ ٹٹدا ہے، تاں اسدی سنسارشیٹ اک پائیپ دو پائیپاں وچّ تبدیل ہون وانگ غلیل وانگ دسدا ہے۔ ایہہ سمستھان پینٹاں دے جوڑے کیہا جاندا ہے۔ جے اک بند رنگ ٹٹدا ہے اتے اسدے دو حصے دوبارہ جڑدے ہن، پھیر اسدی سنسارشیٹ اک پائیپ دی طرحاں بندی ہے جو پہلاں کھلے سرے والا ہندا ہے پھیر جڑ کے دوبارہ اوہی رنگ بن جاندا ہے، پر اک ہور طرحاں دا رنگ وی بن سکدا ہے جو پھلّ وانگ ادھا چکر حاشیے (torus) وانگ دس سکدا ہے جو دو پائیپاں نوں جڑیا ہندا ہے (اک آؤن والا سٹرنگ، اتے دوجا جان والا سٹرنگ درساؤندا ہے)| اک کھلا سٹرنگ جو اجیہا ہی کر رہا ہووے اسدی ورلڈشیٹ انجھ دس سکدی ہے جویں انگوٹھی(annulus) دو پٹیاں نال جڑی ہندی ہے۔
کوانٹم مکینکس وچّ، اک کن دی اد سمبھاونا گنی جاندی ہے جس نال اوہ اک بندو توں دوجے بندو تکّ کجھ نشچت ملاں نوں جوڑ کے لنگھ سکدا ہووے، جناں نوں سمبھاو ایام (probability amplitudes) کیہا جاندا ہے۔ ہریک ایام اک کن دی سنسار ریکھا نال جڑیا ہندا ہے۔ ساریاں سنبھوَ سنسار ریکھاواں دے ایاماں دے جوڑ دی ایہہ ودھی رستہ ایکیکرن (path integration) کہاؤندی ہے۔ سٹرنگ تھیوری وچّ، اک شروعاتی سٹرنگ بنتر توں انتم سٹرنگ بنتر تکّ دیاں سنسارشیٹاں نال سبندھت سنکھیاواں نال، اسے طرحاں سمبھاوناواں دا حساب لگدا ہے۔ ایہہ گلّ سمجھ وچّ ہے کہ سٹرنگ تھیوری کوانٹم پھیلڈ تھیوری نوں بندو-کناں دے سٹرنگاں وچّ بدلن کارن ہور ودھاؤندی ہے۔ جویں کوانٹم پھیلڈ تھیوری وچّ، پھیلڈاں دے پرانے طریقے وچّ کارج دے فنکشن راہیں کھیتر نردھارت کیتا جاندا ہے، اویں ہی ایہہ سٹرنگ تھیوری وچّ جاں نمبو-گوٹو کارج ہو سکدا ہے جاں پولیجوو کارج (Nambu-Goto action or Polyakov action) ہو سکدا ہے۔
برین (Branes)
سودھو
سٹرنگ تھیوری وچّ، اتے ملدیاں جلدیاں جویں سپرگریوٹی تھیوریاں وچّ، اک برین بھوتکی وستو ہندی ہے جو بندو کن دی دھارنا نوں اچے ایاماں لئی برابریکرن کردی ہے۔ جویں، اک بندو کن 0 ایام والے برین وانگ دیکھیا جا سکدا ہے، جدوں کہ سٹرنگ 1 ایامی برین دی طرحاں دیکھیا جا سکدا ہے۔ اچّ ایاماں والے برین سوچنے وی سنبھوَ ہن۔ ایام (dimension) pوچّ ایہناں نوں p-branes کیہا جاندا ہے۔ برین شبد ‘میمبرین’ (membrane) توں بنایا گیا ہے جسدا ارتھ ہے 2ایامی برین|
برین گتی شیل وستواں ہن جو سپیس سمیں وچّ نوں کوانٹم مکینکس دے نیماں مطابق یاترا کر سکدیاں ہن۔ اہنا دا پنج ہندا ہے اتے ہور گن وی ہندے ہن جویں چارج| اک پی-برین سپیس ٹائم وچّ اک (p+1)ایامی گھنپھل (volume) دا صفایا کردا جاندا ہے جسنوں اس برین دا سنسار-گھنپھل (worldvolume) کہندے ہن۔ وگیانی اکثر بجلئی-چمبکتا (الیکٹرومیگنیٹزم) کھیتر دے برابر (analogous) دے کھیتراں نوں سٹڈی کردے ہن جو اک برین دے ورلڈ-وولیؤم وچّ رہندے ہن۔
سٹرنگ تھیوری وچّ، D-branes اک بریناں دی مہتوپورن شرینی ہے جو اسوں پیدا ہندی ہے جدوں کھلے سٹرنگ نوں لیا جاندا ہے۔ جویں اک کھلا سٹرنگ سپیس ٹائم وچّ یاترا کردا ہے،اسدے سرے اک ڈی-برین وچّ ٹکے رہنے چاہیدے ہن۔ ڈی اکھر اس سچ ولّ اشارہ کردا ہے کہ اسیں سسٹم تے اک گنتک شرط لاگوُ کر دندے ہاں جسنوں پہلی قسم دی شرط (Dirichlet boundary condition) کہندے ہاں| سٹرنگ تھیوری دی سٹڈی نے مہتوپورن نتیجیاں دی پریرنا دتی ہے جویں AdS/CFT correspondence(؟)| جسنے کوانٹم پھیلڈ تھیوری دیاں بہت سمسیاواں نوں راہ دکھایا ہے۔
بریناں نوں اک شدھ گنتک نظرئیے توں وی وار وار سٹڈی کیتا جاندا ہے کیونکہ اوہ سامان درپن سمروپتا اتے ستھائی ریکھاگنت (homological mirror symmetry and noncommutative geometry) ورگے وشیاں نال سبندھت ہن۔ گنتک طور تے، برین کجھ نشچت شرینیاں دیاں چیزاں پرستت کر سکدے ہن، جویں اک بہت زیادہ قسماں دی کیلبی-یو (Calabi-Yau) دے میل کھاندے ڈھیراں وچوں کڈھی گئی شرینی جاں نالی (Fukaya) دی شرینی |
ڈی-برین (D-branes)
سودھوسٹرنگ تھیوری وچّ ڈی-برین ودھائیاں ہوئیاں وستواں دی اوہ شرینی ہندی ہے جس تکّ جا کے پہلی حد تکّ دی شرط نال اک کھلا سٹرنگ مکّ سکدا ہے۔ ایہہ ڈائی، لیگ اتے پولچنسکی نے خوجے سن، اتے ہوروانا دوارا 1989 وچّ اکلے نے ہی خوجے سن۔ 1995 وچّ، پولچنسکی نے ڈی بریناں نوں سپرگریوٹی دے حلّ لئی کالے- پی-بریناں دے روپ وچّ پچھانیا| ایہہ اجیہی کھوج سی جسنے دوجی سپرسٹرنگ انقلاب نوں جنم دتا اتے ہولوگراپھک تے ایمّ تھیوری دوہاں لئی پریرنا دتی|
ڈی-برین اپنے خاص ایاماں نال مول روپ وچّ سرینیبدھّ کیتے جاندے ہن، جو ڈی دے نال لکھے نمبر نال درسائے جاندے ہن۔ اک D0-brane سنگل بندو ہندا ہے، D1-brane اک ریکھا ہندی ہے جسنوں D-string وی کہہ سکدے ہاں،اسے طرحاں D2-brane اک ستہِ ہندی ہے، اتے D25-brane بوسونک سٹرنگ تھیوری وچّ اچے توں اچا ایام ہے۔ سیمت کارجہین جھوٹھے برین D(-1)-branes وی ہندے ہن، جو سپیس اتے سمیں دوہاں وچّ سیمت ستھان تے ہندے ہن۔
سدھانتک پچھوکڑ
سودھوسٹرنگ تھیوری دیاں گتی دیاں سمیکرناں نوں ایہہ ضرورت پیندی ہے کہ اک کھلے سریاں والا سٹرنگ نیؤمان حد شرط (Neumann boundary condition) دیاں ، پرکاش دی گتی نال سپیس ٹائم راہیں گزردے وقت مکت سریاں نال سبندھت دو حداں دی شرط وچوں اک ضرور پوری کردا ہووے| جاں پہلی قسم دی شرط (Dirichlet boundary conditions) پوری کردا ہووے، جو سٹرنگ دے سرے بنّ کے رکھدی ہے۔ سٹرنگ دا ہریک حکم-انک (coordinate) ضرور ہی ایہناں شرطاں وچوں اک جاں دوجی شرط پوری کردا ہونا چاہیدا ہے۔ مکس حد والیاں شرطاں دے سٹرنگ وی ہو سکدے ہن، جتھے دوہے سرے NN، DD، ND اتے DN حد شرطاں مندے ہون| جے p ستھانک ایام نیومن حد شرط پوری کردا ہووے، پھیر اوہ سٹرنگ پی-ایامی ہائیپر ستہِ (p-dimensional hyperplane) وچّ گتی کرن لئی بنیا ہو جاندا ہے۔ ایہہ ہائیپر ستہِ Dp-brane دا اک وورن ہے۔
بے شک 0 بنّ دی حد ٹھوس ہندی ہے، پھیر وی کھلے سرے والا سٹرنگ جو ودھ توں ودھ ڈی-ورین تکّ مکّ سکدا ہے، اجیہیاں اوستھاواں رکھدا ہے جو اسدے اتراء چڑاواں نال سبندھت ہندیاں ہن، جسدا ارتھ ہے ڈی-برین گتی شیل وستواں ہن۔ جدوں N D برین لگبھگّ مناسب ہندے ہن، سٹرنگاں دے رنگپٹ سپیکٹرم دی کھچّ بہت امیر بن جاندی ہے۔ اجہیاں اوستھاواں دا اک سیٹ ورلڈ-وولیئماں دی نون-ابیلیئن گیج تھیوری (لاپتا ناپ) پیدا کردا ہے۔ برین دے ہریک آڈے ایام اک ہور اوستھا اک ڈبل شرط گربھ-ایام (N٭N) اوستھا ہندی ہے۔ جے ایہہ گربھ ایام سنّ (commute) کر دتے جان، تاں اوہناں دا وکرنیکرن (diagonalized )ہو سکدا ہے، اتے خود اپنے آپ دی ایگنویلیؤ (eigenvalues) سپیس وچّ N D برین دی ستھتی نوں پربھاشت کردی ہے۔ ہور صاف کہندے ہوئے، برین ستھائی ریکھگنت راہیں درسائے جاندے ہن، جو ودیشی ورتاؤ دکھاؤندے ہن جویں مایہ (Myers) پربھاو، جس وچّ Dp-branes دا اک اکٹھ پھیل کے D(p+2)-brane بن جاندا ہے۔
سنگھنی اورجاہینتا (ٹیکنّ) (Tachyon condensation) اس کھیتر دا مکھ وچار ہے۔ اس پرکریا وچّ کوئی سسٹم لگاتار کن پیدا کر کر کے اپنی اورجا گھٹا سکدا ہے، جو انت نوں سارے سسٹم نوں بھر دندے ہن، تے سسٹم سنگھنا ہو جاندا ہے۔ اشوک سین نے ترک کیتا ہے کہ Type IIB string theory وچّ، ٹیکنّ کنڈنسیشن ( نیویؤ شوارز 3- پرواہ دی غیر حاضری وچّ) D9 اتے anti D9-branes دے اک ڈھیر توں اک منچاہی D-brane بنتر پراپر کرن دی آگیا دندی ہے۔ ایڈورڈ وٹن نے دکھایا کہ اجہیاں بنتراں سپیس سمیں دی کے-تھیوری دوارا شرینی بدھّ کیتیاں جانگیاں| ٹیکن کنڈسیشن اجے بہت گھٹّ سمجھی جاندی ہے۔ ایہہ اک بالکل شدھ سٹرنگ تھیوری دی کمی کارن ہے جو ٹیکنّ دی جھلی-بند اتپتی نوں درسا سکدی ہووے|
دوہرے گن
سودھو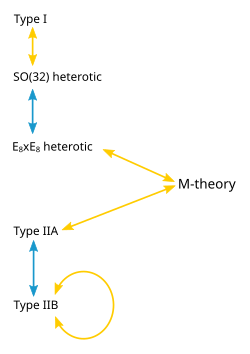
بھوتک وگیان وچّ، دوہرا گن اجیہی پرستھتی ہے جتھے دو وکھرے دسن والے بھوتکی سسٹم اک گمبھیر طریقے نال انبنّ اکو جہے ہو جاندے ہن۔ جے دو تھیوریاں نوں اک دوہرے گن نال ملا دتا جاوے، تاں اسدا مطلب ہے کہ اک تھیوری نوں کسے طرحاں تبدیل کرکے دوجی تھیوری وانگ دسن لگایا جا سکدا ہے۔ پھیر دوویں تھیوریاں تبدیلی ہیٹھاں آپس وچّ ڈبل گن والیاں کہیاں جاندیاں ہن۔ دو تھیوریاں الگّ طریقیاں نال رکھن تے اکو گھٹنا دے وکھرے وکھرے گنتک وورن ہندے ہن۔
تھیوری عوف ایوریتھنگ دے اک سہبھاگی نوں شامل کرن لئی، سٹرنگ تھیوری وکھریاں بھوتکی تھیوریاں درمیان بہت ساریاں دوگلے گناں والیاں اداہرنا مہیا کرواؤندی ہے، جس کارن ایہناں تھیوریاں درمیان سبندھاں نوں سمجھن لئی اک شاستر دے طور تے ورتی جا سکدی ہے۔
S-، T-، اتے U-دوہراپن
سودھوایہہ سٹرنگ تھیوریاں درمیان اوہ دوہرے گن ہندے ہن جو وکھرے ملاں نال سبندھت ہندے ہن۔ وشال تے چھوٹی دوری دے پیمانے، اتے طاقتور اتے کمزور بنّ طاقتاں، اجیہے ملّ ہن جناں نوں ہمیشاں ہی پراتن تے کوانٹم پھجکس دوہاں وچّ اک بھوتکی سسٹم تے وطیرے دیاں بہت وکھریاں شرطاں نال نشان لگایا گیا ہے۔ پر سٹرنگ وشال/ شکتی شالی تے سوخم/کمزور درمیان انتراں نوں ہنیرا کر سکدے ہن، اتے اویں ایہناں 5 وکھریاں بہت مشکل تھیوریاں نوں آپس وچّ رلایا جاندا ہے۔ T-duality وشال تے سوخم دوریاں دے پیمانے نوں سٹرنگ تھیوریاں دے درمیان ملاؤندی ہے، جدونکھ S-duality طاقتور تے کمزور بنّ نوں دے بلاں نوں آپس وچّ رلاؤندی ہے۔ U-duality ایہناں دوویں T-duality اتے S-duality نوں جوڑدی ہے۔
M-تھیوری
سودھوM-تھیوری بھوتک وگیان وچّ اک تھیوری ہے جو سپرسٹرنگ تھیوری دے سارے ستھر روپاں نوں اکٹھا کردی ہے۔ اجیہی اک تھیوری دی ہوند دا انومان سبھ توں پہلاں 1995 دے بسنت موسم وچّ دکھنی کیلیفورنیا دی یونیورسٹی وکھے اک سٹرنگ تھیوری کانفرنس وچّ ایڈورڈ وٹن دوارا لگایا گیا ۔ وٹن نے اعلان نے دوجی سپرسٹرنگ کرانتی دے نام نال جانے جاندے کھوج کارج وچّ اتیجنا دی شروعات کر دتی ۔
1990 توں پہلاں، سٹرنگ وگیانیاں نے منیا کہ 5 وکھریاں سپرسٹرنگ تھیوریاں ہن: type I، type IIA، type IIB، اتے ہیٹروٹک سٹرنگ تھیوری دے دو روپ (SO(32) اتے E8�E8) ہن۔ سوچ ایہہ سی کہ ایہناں 5 امیدوار تھیوریاں وچوں صرف اک شدھ تھیوریؤپھئیورتھنگ ہے، اتے اوہ تھیوری اک اوہ سی جسدی نمر-اورجا-حد، 10 سپیس سمیں دے ایاماں جو 4 تکّ سنگیڑے گئے ہن، ساڈے دیکھے گئے اج دے سنسار دی بھوتک وگیان نال میل کھاندے سن۔ ہن ایہہ منیا جاندا ہے کہ ایہہ تصویر غلط سی تے 5- سپرسٹرنگ تھیوریاں آپس وچّ اپر دسے دوہرے گناں کارن میل کھاندیاں سن۔ ایہناں دوہے گناں دی ہوند سجھاؤندی ہے کہ 5 سٹرنگ تھیوریاں اصل وچّ اک ہور مول M-theory دیاں سپیشل شرینیاں ہن۔
سپیس سماں ایاماں دے مطابق سٹرنگ تھیوری دیاں قسماں
سودھوقسم – Bosonic
سودھو٭ ایام- 26 ٭ وورن -صرف bosons، کوئی fermions نہیں، صرف بلاں تکّ مطلب ہے، پدارتھ نال نہیں، کھلے تے بند سٹرنگ ؛ ٭ مکھ دوش : اک کالپنک کن جسنوں، tachyon، کہندے ہن جو تھیوری وچّ استھرتا پیدا کردا ہے۔
قسم-I
سودھو٭ ایام- 10 ٭ وورن- بلاں تے پدارتھ وچّ سپرسمروپتا Supersymmetry، کھلے تے بند سٹرنگ؛ ٭ کوئی ٹیکن نہیں ؛ ٭ سموہ سمروپتا SO(32) ہے۔
قسم-IIA
سودھو٭ ایام- 10 ٭ وورن- بلاں تے پدارتھ وچّ سپر سمروپتا، صرف بند سٹرنگ ہی D-branes نال بنے ہندے ہن ؛ ٭ کوئی ٹیکن نہیں؛ پنجہین fermions اپنے عکس نال ملدے نہیں ہندے|
قسم- IIB
سودھو٭ ایام- 10 ٭ وورن- بلاں تے پدارتھ وچّ سپرسمروپتا ، صرف بند سٹرنگ ہی D-branes نال بنے ہندے ہن؛ ٭ کوئی ٹیکن نہیں؛ ٭ پنجہین fermions اپنے عکس نال ملدے ہن۔
قسم- HO
سودھو٭ ایام-10 ٭ وورن- بلاں تے پدارتھ وچّ سپرسمروپتا، صرف بند سٹرنگ ہی D-branes نال بنے ہندے ہن؛ ٭ کوئی ٹیکن نہیں؛ ٭ heterotic، یانِ کہ سجے تے کھبے گتی شیل سٹرنگ وکھرے ہندے ہن؛ ٭ سموہ سمروپتا SO(32) ہے۔
قسم- HE
سودھو٭ ایام- 10 ٭ وورن- بلاں تے پدارتھ وچّ سپرسمروپتا، صرف بند سٹرنگ ہی ہندے ہن؛ ٭ کوئی ٹیکن نہیں؛ heterotic، ٭ یانِ کہ سجے تے کھبے گتی شیل سٹرنگ وکھرے ہندے ہن؛ ٭ سموہ سمروپتا E8�E8 ہندی ہے۔
میٹرکس تھیوری
سودھوگنت وچّ اک میٹرکس نمبراں جاں ہور آنکڑے دی اک آئتاکار لڑی ہندی ہے۔ بھوتک وگیان وچّ، اک میٹرکس ماڈل بھوتکی تھیوری دی اک خاص قسم ہے جسدا گنتک فارمولا سوتریکرن میٹرکس دی دھارنا نوں اک مہتوپورن طریقے نال شامل کردا ہے۔ اک میٹرکس ماڈل میٹریسیز دے سیٹ دے ورتاو نوں کوانٹم مکینکس دے ڈھانچے اندر درساؤندا ہے۔
اک میٹرکس ماڈل دی اک مہتوپورن اداہرن ٹوم بینکس، ولی پھشلر، سٹیپھن شینکر، اتے لیؤنارڈ سسکنڈ 1997 وچّ دوارا پرستاوت کیتا BFSS میٹرکس ماڈل ہے۔ ایہہ تھیوری 9 وڈے میٹرکساں دے اک سیٹ دے ورتاؤ نوں درساؤندی ہے۔ اپنے اصلی پیپر وچّ، ایہناں لیکھکاں دے ہور چیزاں دے نہ نال نال دکھایا ہے کہ، اس میٹرکس ماڈل دی نمر اورجا حد 11-ایامی سپر گریوٹی راہیں درسائی جاندی ہے۔ ایہناں گنتیاں منتیاں نے اوہناں نوں ایہہ پرستت کرن دے یوگ بنایا کہ BFSS میٹرکس ماڈل انبنّ M-تھیوری دے سامان ہی ہے۔ BFSS میٹرکس ماڈل نوں اسطراں M-تھیوری دے صحیح فارمولا سوتریکرن لئی اک آدرش مول ماڈل دے طور تے ورتیا جا سکدا ہے اتے اک سرل سیٹنگ وچّ M-تھیوری دیاں وشیشتاواں جانچن لئی اک اوزار دے روپ وچّ ورتیا جا سکدا ہے۔
M-تھیوری دے میٹرکس ماڈل فارمولا سوتریکرن دے وکاس نے بھوتک وگیانیاں نوں سٹرنگ تھیوری اتے نونکمیوٹیٹو جیؤمیٹری نامک گنت دی اک شاکھا درمیان بہت سارے سبندھاں تے وچار کرن لئی مضبوط کر دتا ہے۔ ایہہ وشا سدھارن جیؤمیٹری (ریکھاگنت) دی اک جنرلائیزیشن ہے جس وچّ گنت شاستری نون-کمیوٹیٹو الجبرے توں اوزار ورت کے نویاں ریکھاگنتک دھارناواں پربھاشت کردے ہن ۔ 1998 توں اک پیپر وچّ، الین کونیس، مائیکل آر. ڈگلس، اتے البرٹ شوارز نے دکھایا کہ میٹرکس ماڈل اتے سٹرنگ تھیوری دے کجھ پہلو اک نون-کمیوٹیٹو کوانٹم پھیلڈ تھیوری راہیں درسائے جاندے ہن، جو اک اجیہی سپیشل قسم دی بھوتکی تھیوری ہے جس وچّ سپیسٹائیم نوں نونکمیوٹیٹو جیؤمیٹری (ریکھاگنت) ورتدے ہوئے گنتک طور تے درسایا جاندا ہے۔ اسنے اک پاسے تاں میٹرکس ماڈلاں اتے M-تھیوری درمیان سبندھ ستھاپت کیتے، دوجے پاسے نونکمیوٹیٹو جیؤمیٹری (ریکھاگنت) نال وی سبندھ ستھاپت کیتے ۔ اسنے جلدی ہی نونکمیوٹیٹو جیؤمیٹری (ریکھاگنت) اتے بہت ساریاں ہور بھوتکی تھیوریاں درمیان ہور مہتوپورن سبندھاں دی کھوج لئی وی مجبور کیتا ۔
فالتو ایام
سودھوایاماں دی گنتی
سودھو
سٹرنگ تھیوری دا منموہک گن ایہہ ہے کہ ایہہ وادھو ایاماں دی بھوکھبانی کردی ہے۔ کلاسیکل سٹرنگ تھیوری وچّ ایاماں دی گنتی کسے نرنتر ستھر ماپدنڈ نال پھکس نہیں سی۔ پھیر وی، اک چرستھائی کوانٹم تھیوری بناؤن لئی، سٹرنگ تھیوری نوں اک سپیس ٹائم وچّ رہنا پیندا ہے جس نوں ‘کریٹیکل(ناجک) ایام’ کہندے ہن: اس وچّ کوئی وی چیز دا ٹھوس، دروَ، گیس تے پلازما اوستھا والا گن بدل جاندا ہے؛ اس لئی ساڈے کول سپیس ٹائم دے 26 ایام بوسنوک سٹرنگ دے اتے 10 سپرسٹرنگ دے ہونے ضروری ہن۔ ایہہ انوکولتا کھیتر تھیوری (conformal field theory) والی ورلڈشیٹ دی گتی ورودھی-انوکولتا دے انت نوں یقینی بناؤن لئی ضروری ہے۔ اجوکی سمجھ اشارہ کردی ہے کہ اس شرط نوں پورا کرن لئی ذرا گمبھیر رستے ہندے ہن تے سوکھے رستے گھٹّ ہندے ہن۔ برہمنڈی حلّ ایاماں دی بہت وشال ویرائیٹی وچّ موجود ہندے ہن، اتے ایہہ وکھرے ایام گتی شیل شکتی شالی تبدیلیاں نال سبندھ رکھدے ہن(تلناتمک ہندے ہن)| ایہہ ایام ‘پربھاوشالی کیندری چارج’ دے ہور زیادہ نشچت وکھرے ملّ ہن، کمزور شاسن-پلٹ موڑ (curved regimes) وچّ ایاماں دی کمی دی آزادی دی ڈگری دی گنتی ہے۔
اک اجیہی تھیوری 11 ایامی M-theory ہے، جو سپیس ٹائم دے 11 ایام منگدی ہے، جو عامَ 3 ستھانک ایاماں اتے 4 وقت دے ایام توں الٹ ہے۔ 1980 توں بعد دیاں مول سٹرنگ تھیوریاں اس تھیوری دا خاص کیس درساؤندیاں ہن جتھے 11واں ایام بہت سوخم چکر جاں ریکھا ہندی ہے، تے جیکر ایہناں فارمولیاں بنتراں نوں مول روپ وچّ لیا جاوے، تاں سٹرنگ تھیوری نوں 10ایاماں دی لوڑ پیندی ہے۔ پر پھیر تھیوری ساڈے ورگے برہمنڈ وی درساؤندی ہے، جہناں وچّ سپیس سمیں دے 4 دسنیوگ ایام ہندے ہن اتے اجیہے برہمنڈ وی درساؤندی ہے جہناں وچّ 10 پدھری سپیس دے ایاماں ہندے ہن، اتے جہے کیس وی درساؤندی ہے جتھے کجھ ایاماں وچّ پوزیشن نوں واستوک انک نالوں کمپلیکس نمبر نال درسایا جاندا ہے۔ سٹرنگ تھیوری وچّ سپیسٹائیم دی دھارنا پھکس نہیں کیتی گئی ہے: ایہہ وکھرے ہلاتاں وچّ وکھرے زیادہ ودھیا سوچے گئے ہن۔
میکسویلّ دی الیکٹرومیگنیٹزم دی تھیوری وچّ، جاں آئینسٹائین دی رلیٹوٹو تھیوری وچّ اجیہی کوئی بھوکھبانی نہیں کیتی جاندی: ایہہ تھیوریاں وگیانیاں نوں مانسک طور تے منچاہے ایام بھرن دی ضرورت منگدیاں ہن اتے ایہہ نمبر پھکس رہندا ہے اتے پٹینشل (سمبھاونا، تناؤ، ستھانک، کارجیوگتا) اورجا توں مکت رہندا ہے۔ تکنیکی شبداں وچّ، ایہہ واپردا ہے کیونکہ بھوکھت ایاماں دے ہریک وکھرے نمبر لئی ناپ-اشدھتا gauge anomaly موجود ہندی ہے، تے اس اشدھتا نوں گھٹّ کرن لئی گتی حلّ کرن والیاں سمیکرناں وچّ گمبھیر پٹینسل اورجا نوں شامل کیتا جا سکدا ہے۔ ہور اگے، ‘ناجک ایاماں’ وچّ پٹینشل اورجا دی غیر حاضری دسدی ہے کہ کیوں پدھرے سپیس سمیں حلّ سنبھوَ ہن۔
ایہہ اس گلّ نوں نوٹ کرکے ودھیا سمجھیا جا سکدا ہے کہ اک ستھائی تھیوری وچّ شامل پھوٹون (تکنیکی طور تے اک بل نوں سواری کرواؤن والا کن جو نہ-توڑے جا سکن والی گیج سمٹری نال سبندھت ہے) ضرور پنجہین ہونا چاہیدا ہے۔ سٹرنگ تھیوری دوارا بھوکھت کیتا پھوٹون دا پنج سٹرنگ دی پھوٹون پرستت کرن والی اوستھا تے نربھر ہے۔ ایہہ اورجا کیسیمر پربھاو (Casimir effect) یوگادان کارن ہندی ہے ، جسنوں سٹرنگ وچّ کوانٹم اترء-چڑاؤ توں نام دتا گیا| اس یوگدان دا اکار ایاماں دے نمبر تے نربھر ہے، کیونکہ ایاماں دے وشال نمبر لئی سٹرنگ دی پوزیشن وچّ ہور سنبھوَ اتراء چڑاؤ ہو سکدے ہن۔ اسلئی، پدھرے (فلیٹ)ایام وچّ پھوٹون پنجہین ہووےگا- تے تھیوری ستھر کرن والا صرف کجھ خاص ایاماں دے نمبر لئی ہی ہووےگا| جدوں کیلکلیشن کیتی جاندی ہے تاں ناجک ایام اوستھا 4 نہیں ہندی جویں کوئی امید رکھ سکدا ہے (3 سپیس دے ایام+1 وقت دا ایام)| X-دا اپ سموہ پھوٹون دیاں ریکھک ایام وچّ لہراں برابر ہے۔ بوسوناں دے کیس وچّ فلیٹ سپیس سٹرنگ تھیوریاں 26-ایامی ہن، جدوں کہ سپرسٹرنگ تے ایمّ-تھیوریاں نے ایہناں لئی 10 جاں 11 ایام ہی پدھرے ہلاں لئی رکھے ہن۔
بوسنوکِ سٹرنگ تھیوریاں وچّ 26ایام پولیکوو سمیکرن توں بندے ہن۔ 4 توں زیادہ ایاماں توں شروع کرن لئی ایہہ سوچنا ضروری ہے کہ ایہہ 4 ایامی سپیس ٹائم وچّ کویں سنگیڑیاں جا سکدیاں ہن۔
سوخم سنگڑے پسار
سودھوکالابِ-یاؤ مینیپھولڈ
سودھو
اس سپشٹ انترورودھ نوں حلّ کرن لئی 2 طریقے رکھے گئے ہن۔ پہلا وادھو ایاماں نوں سوخم بناؤنا؛ 6 جاں 7 وادھو ایام انے سوخم ہندے ہن کہ اجوکے پریوگ جانچ نہیں سکدے|
سپرسمٹری دا اچا درجہ پراپت کرن لین لئی، ایہہ سنگڑی ہوئی سوخم سپیس ضرور ہی بہت سپیشل ہونی چاہیدی ہے، جویں اوہناں دی ہولونومی (holonomy) ( گولے تے کسے خاص رستے تے نربھر بل دی سمانتر سواری دی یوگتا)توں پتہ چلدا ہے۔ اک 6ایامی بہو-پرط ضرور ہی SU(3) بنتر والی ہوویگی، جو SU(3) ہولومونی دا سپیشل کیس ہے جس نوں مروڑی نہیں دتی جا سکدی (torsionless)، تے اسنوں کیلبی- یاؤ بہپرت Calabi–Yau سپیس بنا دندا ہے، تے اک 7 ایامی بہت-پرط ضرور ہی G2 بنتر والی ہوویگی ، جس نال اوہ G2 holonomy نال پھیر توں سرل سپیشل کیس بن جاندی ہے۔ اجہیاں سپیساں اس منتوَ لئی سٹڈی کیتیاں گئیاں ہن تاں ہو سٹرنگ تھیوری نوں 4-ایامی سٹینڈرڈ ماڈل نال انشک طور تے گنتی دی سرلتا لئی سپرسمٹری دی دھارنا کر سکن لئی تلناتمک بنایا جا سکے|
بہو-ایامی سپیس نوں سمجھن لئی اک بغیچے دے ربڑ دے پائیپ دی انبنّ سٹینڈرڈ اداہرن ہے۔ جیکر پائیپ ضروری ماترا دی دوری توں دیکھیا جاندا ہے، تاں ایہہ صرف 1 ایامی لگدا ہے جو اسدی لمبائی ہندی ہے۔ سچ مچّ، اک گیند بارے سوچو جو انی چھوٹی ہووے کہ پائیپ وچّ نوں داخل ہو سکدی ہووے| اجیہی گیند نوں پائیپ وچّ سٹن تے ، گیند اک ایام وچّ گھٹّ جاں ودھ گتی کر سکیگی؛ کسے وی پریوگ وچّ، اسیں پائیپ وچّ اجہیاں گینداں سٹن نال، ضروری مہتتا والی گتی صرف 1 ایامی ہوویگی، یانِ کہ، پائیپ دے نال نال ہوویگی| پھیر وی، جویں ہی کوئی پائیپ دے نیڑے پہنچ کے دیکھدا ہے تاں کھوجدا ہے کہ اسدا دوجا ایام وی ہے، جو اسدا گھیرا(گولائی) ہندا ہے۔ تاں پھیر، اسدے اندر تردا اک کیڑا 2 ایاماں وچّ گتی کر سکدا ہووےگا (اتے اسدے اندر اڈدی اک مکھی 3 ایاماں وچّ گتی کر سکدی ہوویگی)| ایہہ وادھو ایام دی "extra dimension" صرف اک تلناتمک نزدیکی پائیپ دے کھیتر توں ہی دیکھی جان جوگی ہوویگی، جاں جے کوئی انسان اس وچّ ضروری ماترا وچّ چھوٹیاں چیزاں سٹدا ہے، تاں دیکھی جا سکیگی| اسے طرحاں، وادھو سوخم ایام صرف چھوٹیاں سوخم دوریاں توں ہی دیکھے جا سکدے ہن، جاں پھیر اجیہے کناں دے نال پریوگ کرکے سنبھوَ ہو سکدا ہے جہناں دیاں ترنگ لمبائیاں wavelengths ( سوخم سنگڑے ایام دے اردھ ویاس دی ووستھا دیاں ویولینتھاں نال) اتّ درجے تکّ ضروری سوخم ہون، جناں نوں کوانٹم مکینکس وچّ اچّ ارجاواں کیہا جاندا ہے۔
برین سنسار کتھا
سودھواک ہور سمبھاونا ایہہ ہے کہ اسیں پورے برہمنڈ دی 3+1 ایامی اپ-سپیس (3 پوزیشن دے ایام+1 وقت دا ایام) وچّ پھس گئے ہاں| سوار کے پوزیشن تے رکھیا پدارتھ اتے یانگ-ملز گیج (Yang–Mills gauge) پھیلڈاں مول روپ وچّ موجود ہونگیاں جے سب-سپیسسماں ( اپّ سپیس ٹائم) زیادہ وڈے برہمنڈ دا اک وشیش سیٹ ہووے| ایہہ سپیشل سیٹ کلابی-یو n-folds وچّ سرو ویاپک ہن اتے ستھانک توڑمروڑ توں بغیر والیاں سبسپیساں دے روپ وچّ درسائے جا سکدے ہن، جو پیپر دی شیٹ دی جھرڑی دے وانگ ہن جاں کسے ودھیا کنچ دی تریڑ وانگ ہن، جسدے گوانڈھ وچّ سپشٹ روپ وچّ سپیشل سبسپیس دے اپنے آپ توں وکھری سپیس ہے۔ پھیر وی، رنڈل تے سندرم دے کم تکّ ایہہ اگیات سی کہ گریوٹی وی سبسپیس سمیں تکّ پجیشن-بدھّ کیتی جا سکدی ہے۔ اسدے نال ہی، سپیس سمیں نوں پرتاں وچّ ووستھ کیتا جا سکدا ہے، جس وچّ وبھنّ ایاماں دیاں پرتاں دا سطر ہووے، جو سانوں 3+1-ایامی چادر وچّ نواس کرن دی آگیا دندا ہے- اجیہے ریکھا گنت قدرتی طور تے کالابی-یو سنگیڑناں وچّ پایا جاندا ہے۔ اجیہے سبسپیسسمے D-برین ہن، جس کارن اجیہے ماڈل برین سنسار سامان جانے جاندے جن| جسنوں ہندی وچّ امک انک آدی کے ٹم کا وورن (ارمبھک انک پرنالی دا وورن) کہندے ہن۔ پنجابی وچّ برین سنسار پرتبمباں دے درش کہندے ہن۔ امک انربھ دے آواز دا وورن وی کیہا جا سکدا ہے۔
لکے ایاماں دا اثر
سودھوکسے وی حالت وچّ، چھپے ایام وچّ کاروائی کردی گریوٹی ہور غیر-گریویٹیشنل بلاں تے پربھاو پاؤندی ہے جویں بجلئی-چمبکتا| اصل وچّ، کلوجا دے شروعاتی کم نے دکھایا کہ 5 ایاماں وچّ جنرل رلیٹیوٹی اصل وچّ بجلئی- چمبکتا دی ہوند درساؤندی ہے۔ پھیر وی، کلابی-یو بہو-پرتاں دے سبھاء کارن، سوخم ایاماں توں کوئی نواں بل نہیں دسدا، پر اوہناں دا اکار اس گلّ تے زوردار پربھاو پاؤندا ہے کہ ساڈے 4-ایامی برہمنڈ وچّ سٹرنگاں درمیان بل کویں دسدے ہن۔ سدھانت وچّ، پھیر وی، سٹینڈرڈ ماڈل نال ملاپ دی ضرورت سمجھ کے اوہناں وادھو ایاماں دے سبھاء نوں پراپت کرنا سنبھوَ ہے، پر ایہہ اجے پریکٹیکل سمبھاونا نہیں بن سکیا۔ گریوٹی دے شدھ ٹیسٹاں راہیں چھپے ایاماں نال سبندھت شدھ سوچنا پراپت کرنا وی سنبھوَ ہے، پر اجے تکّ ایہناں ٹیسٹاں نے اجیہے سوخم ایاماں دی اپرلی حد ہی بنی ہے۔
پرکھ-یوگتاواں اتے پریوگی بھوکھبانیاں
سودھوبے شک تازہ وگیانک کم زیادہتر سٹرنگ تھیوری دا استعمال پارٹیکل پھجکس دے واستبک ماڈل بناؤن لئی دھیان دندے رہے ہن، پھیر وی کئی پرمکھ مشکلاں سٹرنگ تھیوری دے ادھار تے ماڈلاں نوں پرکھنا مشکل کردیاں ہن۔ سبھ توں زیادہ مہتوپورن پلینک لینتھ دا سوخم اکار ہے، جو سٹرنگ دی لمبائی دے نیڑے منیا جاندا ہے (اک سٹرنگ دا وشیش اکار، جتھے سٹرنگ کناں نالوں اسانی نال وکھرے ہو جاندے ہن)| اک ہور مصلیٰ سٹرنگ تھیوری دے پرمانوآں دا کھالیپن ہے، جو ضرور ہی وکھرے طور تے لگبھگّ ہریک گھٹنا نوں انوکول کردا ہے جو اسیں نیویاں اورجاواں تے دیکھدے ہاں۔
سٹرنگ ہارمونکس (String harmonics)
سودھوسٹرنگ تھیوری دا اک نرالا انومان سٹرنگ ہارمونکس دی ہوند ہے۔ ضرورت مطابق اچّ ارجاواں تے، کناں دا سٹرنگ ورگا سبھاء سپشٹّ ہو جاندا ہے۔ سٹرنگ دے اچّ آورتی والے ہارمونکس نال سبندھت، سارے کناں دیاں بھاریاں نقلاں ہونیاں چاہیدیاں ہن۔ ایہہ سپشٹ نہیں ہے ایہہ اورجاواں کویں ہندیاں ہن۔ سبھ توں زیادہ پرمپراگت سٹرنگ ماڈلاں وچّ، ایہہ پلینک اورجا دے نیڑے ہونے چاہیدے ہن، جو نوین پارٹیکل ایکسیلیٹر، LHC وچّ کریاشیل ہون یوگ اورجاواں توں 1014 گنا زیادہ ہے، تے سانوں نیڑے بھوکھ وچّ کسے پارٹیکل ایکسیلیٹر نال اس انومان نوں پرکھنا اسمبھو کردیاں ہن۔ پھیر وی، وشال وادھو ایاماں نال ایہہ سنبھوَ طور تے LHC وچّ پیدا کیتیاں جا سکدیاں ہن، جاں اسدی پہنچ دے اندر دیاں اورجاواں تے پیدا کیتیاں جا سکدیاں ہن۔
فینومینولوجی
سودھواک سدھانتک دلچسپی دا وچار یوگ وچار ہون دے نال نال، سٹرنگ تھیوری واستوک سنسار بھوتک وگیان دے ماڈل رچن لئی ڈھانچہ مہیا کرواؤندی ہے جو جنرل رلیٹیوٹی اتے پارٹیکل پھزکس دا میل کردا ہے۔ پھینومینولوجی سدھانتک بھوتک وگیان دی اوہ شاکھا ہے جس وچّ بھوتک وگیانی ہو زیادہ سنکھیپ سدھانتک وچاراں توں قدرت دے واستوک ماڈل رچدے ہن ۔ سٹرنگ پھینومینولوجی سٹرنگ تھیوری دا اجیہا حصہ ہے جو سٹرنگ تھیوری اتے ادھارت واستوک ماڈل رچن دا یتن کردا ہے۔
کجھ سدھانتک اتے گنتک سمسیاواں کارن، اتے کجھ ایہناں تھیوریاں نوں پریوگک طور تے ٹیسٹ کرن لئی اتی اچّ اورجاواں دی ضرورت ہون کرکے، ہن تکّ کوئی پریوگک ثبوت اپلبدھ نہیں ہے جو سپشٹّ روپ وچّ اشارہ کر سکے کہ ایہناں ماڈلاں وچوں کوئی وی ماڈل قدرت دے وورن دا صحیح مڈھلا وورن ہے۔ اس گلّ نے وگیانک سماج اندر کجھ نوں ایکیکرن پرتِ ایہناں پہنچاں دی الوچنا کرن دا موقع دتا ہے اتے ایہناں کٹھنائیاں اتے نرنتر کھوج دی قیمت اتے سوال کرن لئی مجبور کیتا ہے۔
کاسمولوجی (Cosmology)
سودھواجکلّ دی سمجھ مطابق سٹرنگ تھیوری وشال پدھر تے برہمنڈ دی بنتر بارے انوماناں دی لڑی بناؤندی ہے۔ سٹرنگ تھیوری وچّ کئی حالتاں وچّ وشال پوجیٹو ویکمّ اورجا (واستوک کناں دے جوڑیاں دے جڑ کے ٹٹن نال پیدا ہوئی اورجا) ہے۔ برہمنڈ دے اجیہی اوستھا والے کھیتر چرستھائی پھیلاؤ نامک کریا نال تیزی نال پھیلدے ہن۔ اویں ہی، تھیوری انومان لگاؤندی ہے کہ برہمنڈ دا زیادہتر حصہ تیزی نال پھیل رہا ہے۔ پھیر وی، ایہہ پھیل رہیاں اوستھاواں ستھائی نہیں ہن، اتے نیویں ویکمّ اورجا دے بلبلیاں دی نیوکلیئیشن راہیں لیک ہو سکدی ہے۔ کیونکہ برہمنڈ دا ساڈا ستھانک کھیتر تیزی نال پھیل نہیں رہا، سٹرنگ تھیوری انومان لگاؤندی ہے کہ اسیں اجیہے بلبلے دے اندر ہاں| بلبلیاں دے اندر دی برہمنڈ دی ستھانک گولائی جو اک پرکھیوگ انومان ہے تے اس کریا دوارا بندی ہے، نیگیٹو ہندی ہے۔ ہور اگے، بلبلے انت نوں بلبلیاں دے باہر مکھ ویکمّ دا نرمان کردے ہن تے اس نال ٹکراؤندے ہن۔ ایہہ ٹکراؤ سنبھوَ طور تے برہمنڈ وگیان وچّ دسنیوگ نوشان چھڈدے ہن۔ پھیر وی، ایہہ سنبھوَ ہے کہ ایہناں وچوں کوئی وی دیکھیا نہیں جا سکیگا جیکر ستھانک گولائی بہت سوخم ہوویگی اتے ٹکراؤ بہت گھٹّ ہونگے|
کجھ حالتاں وچّ، پھیلاؤ دے انت دے نیڑے پیدا ہوئے مڈھلے سٹرنگ کھگولک انپاتاں تکّ کھچے جا سکدے ہن۔ ایہہ برہمنڈی سٹرنگ کئی طریقیاں نال دیکھے جا سکدے ہن، جویں اوہناں دے گروتاکرشن لینسنگ پربھاواں راہیں|( گروتاکیشن لینسنگ= دور دے سومے اتے درشک وچکار گلیکسیاں دے جھنڈاں دیاں پلیٹاں دی ونڈ)| پھیر وی، کجھ پھیلڈ تھیوریاں ایہہ انومان وی لگاؤندیاں ہن کہ برہمنڈی سٹرنگ پھیلڈ بنتراں وچّ سمستھانک (topological) نقصاں توں پیدا ہندے ہن۔
سپر سیمیٹرا(Supersymmetry)
سودھوجیکر پریوگک طور تے ثابت ہو جاندا ہے، تاں سپرسمروپتا وی سنیوگوش گواہ دے طور تے لئی جا سکدی ہے، کیونکہ ساریاں ستھائی سٹرنگ تھیوریاں سپرسمروپ ہن۔ پھیر وی، وشال ہاڈرن کولائیڈر LHC وچّ کریایوگ اورجاواں تے سپرسمروپ کناں دی غیر حاضری ضروری نہیں ہے کہ سٹرنگ تھیوری نوں ثابت نہ کرے، کیونکہ جس اورجا پیمانے تے سپرسمروپتا ٹٹّ جاندی ہے اوہ چنگی طرحاں ایکسلریٹر دے دائرے توں اپر ہو سکدا ہے۔
AdS/CFT میل
سودھوanti-de Sitter/conformal field theory (AdS/CFT) میل اک سبندھ ہے جسدے مطابق کجھ حالتاں وچّ سٹرنگ تھیوری کوانٹم پھیلڈ تھیوری برابر ہے۔ زیادہ سنکھیپ وچّ کہندے ہوئے، سٹرنگ تھیوری جاں ایمّ-تھیوری نوں اک anti-de Sitter پچھوکڑ تے دیکھنا ہے۔ اسدا ارتھ ہے کہ پلاڑ وچّ آئینسٹائین دی سمیکرن دے کجھ ہلاں نوں وگاڑ کے سپیسسمیں دا ریکھا گنت بنایا جاندا ہے۔ اس سیٹنگ وچّ، سپیس سمیں دی حد پربھاشت کرنی سنبھوَ ہے۔ AdS/CFT میل درساؤندا ہے کہ اک کوانٹم پھیلڈ تھیوری لئی اس حد نوں سپیس سماں کیہا جا سکدا ہے، اتے ایہہ پھیلڈ تھیور وشال گروکارشن تھیوری دے نال اس سمجھ انوسار برابر ہے جس وچّ، اک تھیوری دے حساب کتاب نوں دوجی تھیوری دے حساب کتاب وچّ انوواد کرن دا شبدکوش ہووے|
میل دیاں اداہرناں
سودھوAdS/CFT میل دی سبھ توں پرسدھ اداہرن مطابق Type IIB سٹرنگ تھیوری AdS5 � S5 دی پیداور تے 4-ایامی انوروپ حد تے N = 4 super Yang–Mills تھیوری برابر ہے۔ اس میل دے اک ہور انوبھوَ انوسار AdS4 � S7 اتے ایمّ-تھیوری 3-ایاماں وچّ ABJM superconformal پھیلڈ تھیوری برابر ہے۔ اجے اک ہور انوبھوَ انوسار AdS7 � S4 اتے ایمّ-تھیوری 6-ایاماں وچّ (2،0)-تھیوری برابر ہے۔
کوانٹم کروموڈائنامکس لئی استعمال
سودھوکیونکہ ایہہ سٹرنگ تھیوری دا سدھارن کوانٹم پھیلڈ تھیوری نال میل کردا ہے، AdS/CFT میل نوں کوانٹم پھیلڈ تھیوری وچّ حساب لگاؤن لئی سدھانتک اوزار دے طور تے ورتیا جا سکدا ہے۔ اداہرن وجوں، اس میل نوں کوارک-گلوؤن پلازما دے ادھٔین لئی ورتیا گیا ہے، جو پارٹیکل ایکسیلیٹر وچّ پیدا ہوئے پدارتھ دی عجیب اوستھا ہے۔
کوارک-گلوؤن پلازما دی بھوتک وگیان کوانٹم کروموڈائنامکس راہیں چلائی جاندی ہے، جو طاقتور نیوکلیئر بل دی مڈھلی تھیوری ہے، پر ایہہ تھیوری کوارک-گلوؤن پلازما دے معاملے وچّ گنتک طور تے سمسیاواں راہیں صحیح نہیں بیٹھدی| کوارک-گلوؤن پلازما دیاں کجھ وشیشتاواں نوں سمجھن لئی، سدھانتوادیاں نے اسلئی AdS/CFT میل دی ورتو کیتی ہے۔ اس میل دا اک روپ سٹرنگ تھیوری نوں اک نشچت سپرسمروپ گیز تھیوری نال ملاؤندا ہے جس نوں N = 4 super Yang–Mills theory کہندے ہن۔ بعد وچّ لکھی تھیوری کوانٹم کروموڈائنامکس لئی لگبھگّ چنگی سمانتا موہئیا کرواؤندی ہے۔ کوئی وی اسطراں کوارک-گلوؤن پلازما نال سبندھت سمسیاواں نوں سٹرنگ تھیوری دیاں سمسیاواں وچّ بدل سکدا ہے جو زیادہ اسان ہن۔ ایہہ طریقے ورتدے ہوئے، سدھانتوادیاں نے کوارک-گلوؤن پلازما دا کٹیا ہویا دلدلپنا (shear viscosity) منیا ہے۔ 2008 وچّ، برکہیون راشٹری پریوگشالا (Brookhaven National Laboratory) وچّ تلناتمک بھاری آئؤن کولائیڈر (Relativistic Heavy Ion Collider) تے ایہہ انومان ثابت کیتے گئے ہن۔
سنگھنے مادےوالی فزکس لئی استعمال
سودھواسدے نال نال، سٹرنگ تھیوری دے طریقے سنگھنے پدارتھ دی بھوتک وگیان دیاں سمسیاواں تے وی لاگوُ کیتے گئے ہن۔ کجھ سنگھنے پدارتھ دیاں پرنالیاں کوانٹم پھیلڈ تھیوری دے طریقیاں دی ورتوں نال سمجھنیاں مشکل ہن، اتے AdS/CFT میل بھوتک وگیانیاں نوں سٹرنگ تھیوری دی بھاشا وچّ ایہناں پرنالیاں نوں چنگی طرحاں سمجھن دی اگیا دندا ہے۔ سٹرنگ تھیوری دے طریقیاں راہیں اک سپرپھلڈّ دی اک انسلیٹر وچّ تبدیلی دی ویاکھیا راہیں کافی سفلتا حاصل ہوئی ہے۔
گنت نال سبندھ
سودھوسدھانتک بھوتک وگیان دیاں پربھاوشالی کھوجاں وچّ ہور جوڑدے ہوئے، سٹرنگ تھیوری نے سدھّ-گنت دے وچّ بہت سارا وکاس کیتا ہے۔ سدھانتک بھوتک وگیان دے وکست ہو رہے وچاراں وانگ، سٹرنگ تھیوری کول فلحال کٹھور گنتک بنتراں نہیں ہن جس وچّ اسدے سارے سنکلپ سنکھیپ روپ وچّ درسائے جا سکن۔ نتیجے وجوں، جو بھوتک وگیانی سٹرنگ تھیوری دا ادھٔین کردے ہن،اکثر دسدیاں وبھنّ گنتک ڈھانچیاں درمیان سبندھاں دا انومان لاؤن لئی بھوتکی سہج-گیان دوارا ہی گائیڈ کیتے جاندے ہن جو تھیوری دے وکھرے حصیاں دی بنتر لئی ورتے جاندے ہن۔ ایہہ انومان بعد وچّ گنتشاستریاں دوارا ثابت کیتے جاندے ہن، اتے اس طرحاں، سٹرنگ تھیوری نے شدھ گنت وچّ نویں وچاراں دے سومے دے روپ وچّ کم کیتا ہے۔
مرر سیمیٹری (Mirror symmetry)
سودھو
درپن سمروپتا دی کھوج راہیں سٹرنگ تھیوری نے گنت نوں پربھاوت کیتا ہے۔ سٹرنگ تھیوری وچّ، ادرش ستھانک ایاماں دا اکار عامَ طور تے کالابِ-یاؤ بہو-پرتاں نامک گنتک چیزاں وچّ سنکیتک شبداں وچّ بدلیا جاندا ہے (encoded)| ایہہ شدھ گنت وچّ دلچسپی والیاں ہن، تے سٹرنگ تھیوری راہیں پھجکس دے یتھارتھوادی ماڈلاں دی بنتر لئی ورتیاں جاندیاں ہن۔ 1980ویں دہاکے دے اخیر وچّ، ایہہ نوٹ کیتا گیا کہ کسے دتے ہوئے پھجکل ماڈل لئی، سبندھت نرالی کالابِ-یاؤ بہو-پرط بناؤنی سنبھوَ ہے۔ سگوں، ایہہ وی کھوجیا گیا کہ دو کالابِ-یاؤ بہو-پرتاں اجو پھجکس بناؤندیاں ہن۔ ایہناں بہو-پرتاں نوں اک دوجی دیاں درپن کیہا گیا| وبھنّ کالابِ-یاؤ بہو-پرتاں درمیان اس درپن سمروپتا سبندھ دی ہوند دیاں مہتوپورن گنتک لڑیاں بندیاں ہن کیونکہ ایہہ گنتی سوچک الجبرک ریکھاگنت دیاں کئی سمسیاواں حلّ کرن وچّ گنتشاستریاں دی مددّ کردا ہے۔ اجکلّ گنتشاستری اجے وی بھوتک وگیانیاں دے سہج گیان تے ادھارت درپن سمروپتا دی گنتک سمجھ وکست کرن وچّ لگے ہوئے ہن۔
شکھر اپریٹر بیجگنت (Vertex operator algebras)
سودھودرپن سمروپتا توں علاوہ، سٹرنگ تھیوری دے شدھ گنت وچّ اپیوگاں وچّ شکھر اپریٹر بیجگنت (Vertex operator algebras) دی تھیوری شامل ہے۔ اداہرن وجوں، سٹرنگ تھیوری دے وچار 1992 وچّ رچرڈ بورچرڈز دوارا monstrous moonshine انومان نوں ثابت کرن ورتے گئے جو monster group (گروپ تھیوری وچّ پیدا ہوئی اک بنتر)تے modular functions (نمبر تھیوری وچّ مہتوپورن پھنکشناں دی اک شرینی) نال سبندھت سی۔
حوالے
سودھونوٹس
سودھوہور حوالے
سودھوحوالہ کتاب لسٹ
سودھو- (2009) Dirichlet Branes and Mirror Symmetry. American Mathematical Society. ISBN 978-0-8218-3848-8.
- Banks, Tom; Fischler, Willy; Schenker, Stephen; Susskind, Leonard (1997). "M theory as a matrix model: A conjecture". Physical Review D 55 (8): 5112–5128. doi:. Bibcode: 1997PhRvD..55.5112B.
- (2007) String theory and M-theory: A modern introduction. Cambridge University Press. ISBN 978-0-521-86069-7.
- Bekenstein, Jacob (1973). "Black holes and entropy". Physical Review D 7 (8): 2333–2346. doi:. Bibcode: 1973PhRvD...7.2333B.
- Bergshoeff, Eric; Sezgin, Ergin; Townsend, Paul (1987). "Supermembranes and eleven-dimensional supergravity". Physics Letters B 189 (1): 75–78. doi:. Bibcode: 1987PhLB..189...75B.
- Borcherds, Richard (1992). "Monstrous moonshine and Lie superalgebras". Inventiones Mathematicae 109 (1): 405–444. doi:. Bibcode: 1992InMat.109..405B.
- Candelas, Philip; de la Ossa, Xenia; Green, Paul; Parks, Linda (1991). "A pair of Calabi–Yau manifolds as an exactly soluble superconformal field theory". Nuclear Physics B 359 (1): 21–74. doi:. Bibcode: 1991NuPhB.359...21C.
- Candelas, Philip; Horowitz, Gary; Strominger, Andrew; Witten, Edward (1985). "Vacuum configurations for superstrings". Nuclear Physics B 258: 46–74. doi:. Bibcode: 1985NuPhB.258...46C.
- Castro, Alejandra; Maloney, Alexander; Strominger, Andrew (2010). "Hidden conformal symmetry of the Kerr black hole". Physical Review D 82 (2). doi:. Bibcode: 2010PhRvD..82b4008C.
- سانچہ:Cite arXiv
- Connes, Alain (1994). Noncommutative Geometry. Academic Press. ISBN 978-0-12-185860-5.
- Connes, Alain; Douglas, Michael; Schwarz, Albert (1998). "Noncommutative geometry and matrix theory". Journal of High Energy Physics 19981 (2): 003. doi:. Bibcode: 1998JHEP...02..003C.
- Conway, John; Norton, Simon (1979). "Monstrous moonshine". Bull. London Math. Soc. 11 (3): 308–339. doi:.
- Cremmer, Eugene; Julia, Bernard; Scherk, Joel (1978). "Supergravity theory in eleven dimensions". Physics Letters B 76 (4): 409–412. doi:. Bibcode: 1978PhLB...76..409C.
- de Haro, Sebastian; Dieks, Dennis; 't Hooft, Gerard; Verlinde, Erik (2013). "Forty Years of String Theory Reflecting on the Foundations". Foundations of Physics 43 (1): 1–7. doi:. Bibcode: 2013FoPh...43....1D.
- (1999) Quantum Fields and Strings: A Course for Mathematicians 1. American Mathematical Society. ISBN 978-0821820124.
- Duff, Michael (1996). "M-theory (the theory formerly known as strings)". International Journal of Modern Physics A 11 (32): 6523–41. doi:. Bibcode: 1996IJMPA..11.5623D.
- Duff, Michael (1998). "The theory formerly known as strings". Scientific American 278 (2): 64–9. doi:.
- Duff, Michael; Howe, Paul; Inami, Takeo; Stelle, Kellogg (1987). "Superstrings in D=10 from supermembranes in D=11". Nuclear Physics B 191 (1): 70–74. doi:. Bibcode: 1987PhLB..191...70D.
- (2004) Abstract Algebra. Wiley. ISBN 978-0-471-43334-7.
- سانچہ:Cite arXiv
- Eguchi, Tohru; Ooguri, Hirosi; Tachikawa, Yuji (2011). "Notes on the K3 surface and the Mathieu group M24". Experimental Mathematics 20 (1): 91–96. doi:.
- (1988) Vertex Operator Algebras and the Monster, Pure and Applied Mathematics 134. Academic Press. ISBN 0-12-267065-5.
- Moonshine Beyond the Monster: The Bridge Connecting Algebra, Modular Forms, and Physics. Cambridge University Press.
- Givental, Alexander (1996). "Equivariant Gromov-Witten invariants". International Mathematics Research Notices 1996 (13): 613–663. doi:.
- Givental, Alexander (1998). "A mirror theorem for toric complete intersections". Topological field theory, primitive forms and related topics: 141–175. doi:. ISBN 978-1-4612-6874-1.
- Gubser, Steven; Klebanov, Igor; Polyakov, Alexander (1998). "Gauge theory correlators from non-critical string theory". Physics Letters B 428: 105–114. doi:. Bibcode: 1998PhLB..428..105G.
- Guica, Monica; Hartman, Thomas; Song, Wei; Strominger, Andrew (2009). "The Kerr/CFT Correspondence". Physical Review D 80 (12). doi:. Bibcode: 2009PhRvD..80l4008G.
- Hawking, Stephen (1975). "Particle creation by black holes". Communications in Mathematical Physics 43 (3): 199–220. doi:. Bibcode: 1975CMaPh..43..199H.
- Hawking, Stephen (2005). "Information loss in black holes". Physical Review D 72 (8). doi:. Bibcode: 2005PhRvD..72h4013H.
- Hořava, Petr; Witten, Edward (1996). "Heterotic and Type I string dynamics from eleven dimensions". Nuclear Physics B 460 (3): 506–524. doi:. Bibcode: 1996NuPhB.460..506H.
- (2003) Mirror Symmetry. American Mathematical Society. ISBN 0-8218-2955-6. Archived 2006-09-19 at the وے بیک مشین
- Hull, Chris; Townsend, Paul (1995). "Unity of superstring dualities". Nuclear Physics B 4381 (1): 109–137. doi:. Bibcode: 1995NuPhB.438..109H.
- Kapustin, Anton; Witten, Edward (2007). "Electric-magnetic duality and the geometric Langlands program". Communications in Number Theory and Physics 1 (1): 1–236. doi:. Bibcode: 2007CNTP....1....1K.
- Klarreich، Erica. «Mathematicians chase moonshine's shadow». Quanta Magazine. دریافتشده در March 2015. تاریخ وارد شده در
|accessdate=را بررسی کنید (کمک) - Klebanov, Igor; Maldacena, Juan (2009). "Solving Quantum Field Theories via Curved Spacetimes" (PDF). Physics Today 62: 28–33. doi:. Bibcode: 2009PhT....62a..28K. http://www.sns.ias.edu/~malda/Published.pdf. Retrieved on
- Kontsevich, Maxim (1995). "Homological algebra of mirror symmetry". Proceedings of the International Congress of Mathematicians: 120–139. Bibcode: 1994alg.geom.11018K.
- Kovtun, P. K.; Son, Dam T.; Starinets, A. O. (2001). "Viscosity in strongly interacting quantum field theories from black hole physics". Physical Review Letters 94 (11): 111601. doi:. PMID 15903845. Bibcode: 2005PhRvL..94k1601K.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1997). "Mirror principle, I". Asian Journal of Math 1: 729–763. Bibcode: 1997alg.geom.12011L.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1999a). "Mirror principle, II". Asian Journal of Math 3: 109–146. Bibcode: 1999math......5006L.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (1999b). "Mirror principle, III". Asian Journal of Math 3: 771–800. Bibcode: 1999math.....12038L.
- Lian, Bong; Liu, Kefeng; Yau, Shing-Tung (2000). "Mirror principle, IV". Surveys in Differential Geometry 7: 475–496. doi:. Bibcode: 2000math......7104L.
- Luzum, Matthew; Romatschke, Paul (2008). "Conformal relativistic viscous hydrodynamics: Applications to RHIC results at سانچہ:Radical=200 GeV". Physical Review C 78 (3). doi:.
- Maldacena, Juan (1998). "The Large N limit of superconformal field theories and supergravity". Advances in Theoretical and Mathematical Physics 2: 231–252. doi:. Bibcode: 1998AdTMP...2..231M.
- Maldacena, Juan (2005). "The Illusion of Gravity". Scientific American 293 (5): 56–63. doi:. PMID 16318027. Bibcode: 2005SciAm.293e..56M. http://www.sns.ias.edu/~malda/sciam-maldacena-3a.pdf. Retrieved on
- Maldacena, Juan; Strominger, Andrew; Witten, Edward (1997). "Black hole entropy in M-theory". Journal of High Energy Physics 1997 (12). doi:.
- Merali, Zeeya (2011). "Collaborative physics: string theory finds a bench mate". Nature 478 (7369): 302–304. doi:. PMID 22012369. Bibcode: 2011Natur.478..302M.
- Moore, Gregory (2005). "What is ... a Brane?" (PDF). Notices of the AMS 52: 214. http://www.ams.org/notices/200502/what-is.pdf. Retrieved on جون ۲۰۱۳.
- Nahm, Walter (1978). "Supersymmetries and their representations". Nuclear Physics B 135 (1): 149–166. doi:. Bibcode: 1978NuPhB.135..149N.
- Nekrasov, Nikita; Schwarz, Albert (1998). "Instantons on noncommutative R4 and (2,0) superconformal six dimensional theory". Communications in Mathematical Physics 198 (3): 689–703. doi:. Bibcode: 1998CMaPh.198..689N.
- Ooguri, Hirosi; Strominger, Andrew; Vafa, Cumrun (2004). "Black hole attractors and the topological string". Physical Review D 70 (10). doi:.
- Polchinski, Joseph (2007). "All Strung Out?". American Scientist. http://www.americanscientist.org/bookshelf/pub/all-strung-out. Retrieved on
- Penrose, Roger (2005). The Road to Reality: A Complete Guide to the Laws of the Universe. Knopf. ISBN 0-679-45443-8.
- Randall, Lisa; Sundrum, Raman (1999). "An alternative to compactification". Physical Review Letters 83 (23): 4690–4693. doi:. Bibcode: 1999PhRvL..83.4690R.
- Sachdev, Subir (2013). "Strange and stringy". Scientific American 308 (44): 44–51. doi:. Bibcode: 2012SciAm.308a..44S.
- Seiberg, Nathan; Witten, Edward (1999). "String Theory and Noncommutative Geometry". Journal of High Energy Physics 1999 (9): 032. doi:. Bibcode: 1999JHEP...09..032S.
- Sen, Ashoke (1994a). "Strong-weak coupling duality in four-dimensional string theory". International Journal of Modern Physics A 9 (21): 3707–3750. doi:. Bibcode: 1994IJMPA...9.3707S.
- Sen, Ashoke (1994b). "Dyon-monopole bound states, self-dual harmonic forms on the multi-monopole moduli space, and SL(2,Z) invariance in string theory". Physics Letters B 329 (2): 217–221. doi:. Bibcode: 1994PhLB..329..217S.
- Smolin, Lee (2006). The Trouble with Physics: The Rise of String Theory, the Fall of a Science, and What Comes Next. New York: Houghton Mifflin Co.. ISBN 0-618-55105-0.
- Strominger, Andrew (1998). "Black hole entropy from near-horizon microstates". Journal of High Energy Physics 1998 (2): 009. doi:. Bibcode: 1998JHEP...02..009S.
- Strominger, Andrew; Vafa, Cumrun (1996). "Microscopic origin of the Bekenstein–Hawking entropy". Physics Letters B 379 (1): 99–104. doi:. Bibcode: 1996PhLB..379...99S.
- Strominger, Andrew; Yau, Shing-Tung; Zaslow, Eric (1996). "Mirror symmetry is T-duality". Nuclear Physics B 479 (1): 243–259. doi:. Bibcode: 1996NuPhB.479..243S.
- (2005) The Cosmic Landscape: String Theory and the Illusion of Intelligent Design. Back Bay Books. ISBN 978-0316013338.
- (2008) The Black Hole War: My Battle with Stephen Hawking to Make the World Safe for Quantum Mechanics. Little, Brown and Company. ISBN 978-0-316-01641-4.
- (1984) General Relativity. University of Chicago Press. ISBN 978-0-226-87033-5.
- (1987) Anthropic bound on the cosmological constant 59. Physical Review Letters, 2607.
- Witten, Edward (1995). "String theory dynamics in various dimensions". Nuclear Physics B 443 (1): 85–126. doi:. Bibcode: 1995NuPhB.443...85W.
- Witten, Edward (1998). "Anti-de Sitter space and holography". Advances in Theoretical and Mathematical Physics 2: 253–291. Bibcode: 1998AdTMP...2..253W.
- سانچہ:Cite arXiv
- Woit, Peter (2006). Not Even Wrong: The Failure of String Theory and the Search for Unity in Physical Law. Basic Books, 105. ISBN 0-465-09275-6.
- (2010) The Shape of Inner Space: String Theory and the Geometry of the Universe's Hidden Dimensions. Basic Books. ISBN 978-0-465-02023-2.
- Zee, Anthony (2010). Quantum Field Theory in a Nutshell, 2nd, Princeton University Press. ISBN 978-0-691-14034-6.
- (2009) A First Course in String Theory. Cambridge University Press. ISBN 978-0-521-88032-9.
ہور اگے پڑائی
سودھولوک پرچار
سودھوسرو سدھارن
سودھو- Greene, Brian (2003). The Elegant Universe: Superstrings، Hidden Dimensions، and the Quest for the Ultimate Theory. New York: W.W. Norton & Company. ISBN 0-393-05858-1.
- Greene, Brian (2004). The Fabric of the Cosmos: Space، Time، and the Texture of Reality. New York: Alfred A. Knopf. ISBN 0-375-41288-3.
الوچناتمک
سودھو- Penrose, Roger (2005). The Road to Reality: A Complete Guide to the Laws of the Universe. Knopf. ISBN 0-679-45443-8.
- Smolin, Lee (2006). The Trouble with Physics: The Rise of String Theory، the Fall of a Science، and What Comes Next. New York: Houghton Mifflin Co.. ISBN 0-618-55105-0.
- Woit, Peter (2006). Not Even Wrong: The Failure of String Theory And the Search for Unity in Physical Law. London: Jonathan Cape &: New York: Basic Books. ISBN 978-0-465-09275-8.
کتاباں
سودھوطبعیتداناں واسطے
سودھو- (2007) String Theory and M-theory: A Modern Introduction. Cambridge University Press. ISBN 978-0-521-86069-7.
- (2012) Superstring theory. Vol. 1: Introduction. Cambridge University Press. ISBN 978-1107029118.
- (2012) Superstring theory. Vol. 2: Loop amplitudes، anomalies and phenomenology. Cambridge University Press. ISBN 978-1107029132.
- (1998) String Theory Vol. 1: An Introduction to the Bosonic String. Cambridge University Press. ISBN 0-521-63303-6.
- Polchinski, Joseph (1998). String Theory Vol. 2: Superstring Theory and Beyond. Cambridge University Press. ISBN 0-521-63304-4.
- (2009) A First Course in String Theory. Cambridge University Press. ISBN 978-0-521-88032-9.
ریاضی داناں واسطے
سودھو- (1999) Quantum Fields and Strings: A Course for Mathematicians، Vol. 2. American Mathematical Society. ISBN 978-0821819883.